Предмет: Алгебра,
автор: sqqqqqffda
найдите первую и вторую производные
![\sqrt[3]{(\frac{x+1}{x-1})^2 } \sqrt[3]{(\frac{x+1}{x-1})^2 }](https://tex.z-dn.net/?f=%5Csqrt%5B3%5D%7B%28%5Cfrac%7Bx%2B1%7D%7Bx-1%7D%29%5E2+%7D)
Ответы
Автор ответа:
0
Надеюсь, нигде в арифметике не ошибся. Если что, напиши.
Приложения:
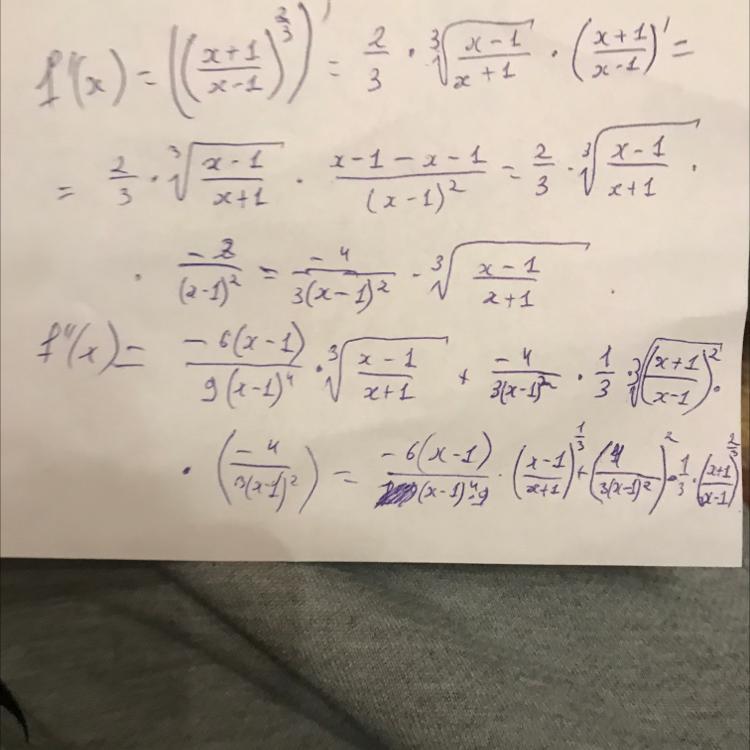
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Биология,
автор: rusa020102
Предмет: Литература,
автор: ofomich
Предмет: Математика,
автор: слава40
Предмет: Физика,
автор: Manvey
Предмет: Математика,
автор: 4ae444ka