Предмет: Математика,
автор: Kapirat
Найти производную второго порядка y"xx, от функции заданной параметрически
Приложения:
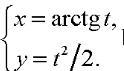
Ответы
Автор ответа:
1
Ответ:
1.
2.
Похожие вопросы
Предмет: Биология,
автор: VityaMatyz
Предмет: Математика,
автор: вик27
Предмет: Математика,
автор: dubovik05
Предмет: Информатика,
автор: AkemiAyato
Предмет: Алгебра,
автор: ева542