Предмет: Алгебра,
автор: hkin1
Помогите с уравнением пожалуйста. Пункт а
Приложения:
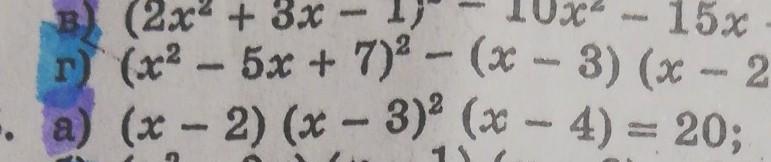
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Введём замену:
Перепишем уравнение с учётом замены:
Решим уравнение при помощи теоремы Виета:
Вернёмся к замене:
pinguinbird:
Отличное решение!
Спасибо.
Автор ответа:
0
не подходит, т.к. квадрат любого числа больше либо равен 0\\
значит
Ответ:
Похожие вопросы
Предмет: Математика,
автор: oliferov2005
Предмет: Русский язык,
автор: kastet1
Предмет: Русский язык,
автор: yulia3077
Предмет: Математика,
автор: 891672Мехрангез
Предмет: Математика,
автор: kolbaska4