Предмет: Алгебра,
автор: Mukuto
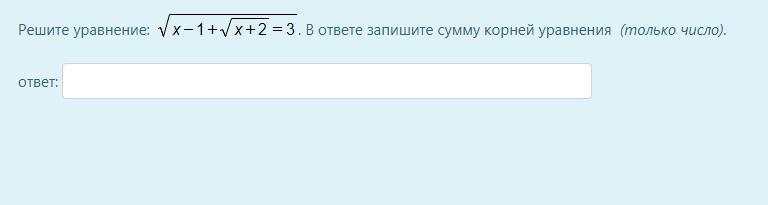
----Решите уравнение----
Приложения:
Ответы
Автор ответа:
1
Mukuto:
Не правильно
Похожие вопросы
Предмет: Английский язык,
автор: 3ira
Предмет: Русский язык,
автор: medvedeva594
Предмет: Русский язык,
автор: кактус1234
Предмет: Математика,
автор: бешикташ5
Предмет: Математика,
автор: omusheg