..............................................................

Ответы
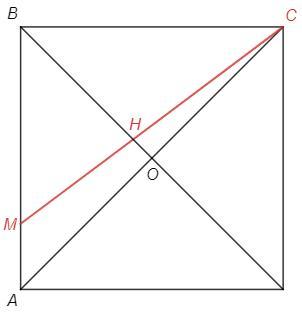
Правильная 4-угольная пирамида - в основании квадрат, вершина проецируется в точку пересечения диагоналей основания.
Опустим перпендикуляр KH на основание.
Точка H на BO
(В правильной пирамиде радиусы основания являются проекциями боковых ребер.)
Искомое сечение проходит через KH.
(Перпендикулярная плоскость проходит через перпендикулярную прямую.)
Проверим точки M, H, C по теореме Менелая:
AM/MB *BH/HO *OC/CA =1
KH||SO => BH/HO=BK/KS =6/1 (т о пропорциональных отрезках)
2/6 *6/1 *1/2 =1
Для точек M, H, C выполняется теорема Менелая, следовательно они лежат на одной прямой.
OA=AB√2/2 =4√2
SO =√(SA^2 -OA^2) =√(49-32) =√17 (т Пифагора)
KH||SO => △BKH~△BSO => KH/SO=BK/BS =6/7 => KH =6/7 *√17
MC =√(MB^2 +BC^2) =10 (т Пифагора)
S(MKC) =1/2 MC*KH =1/2 *10 *6/7 *√17 =30/7 *√17