Question

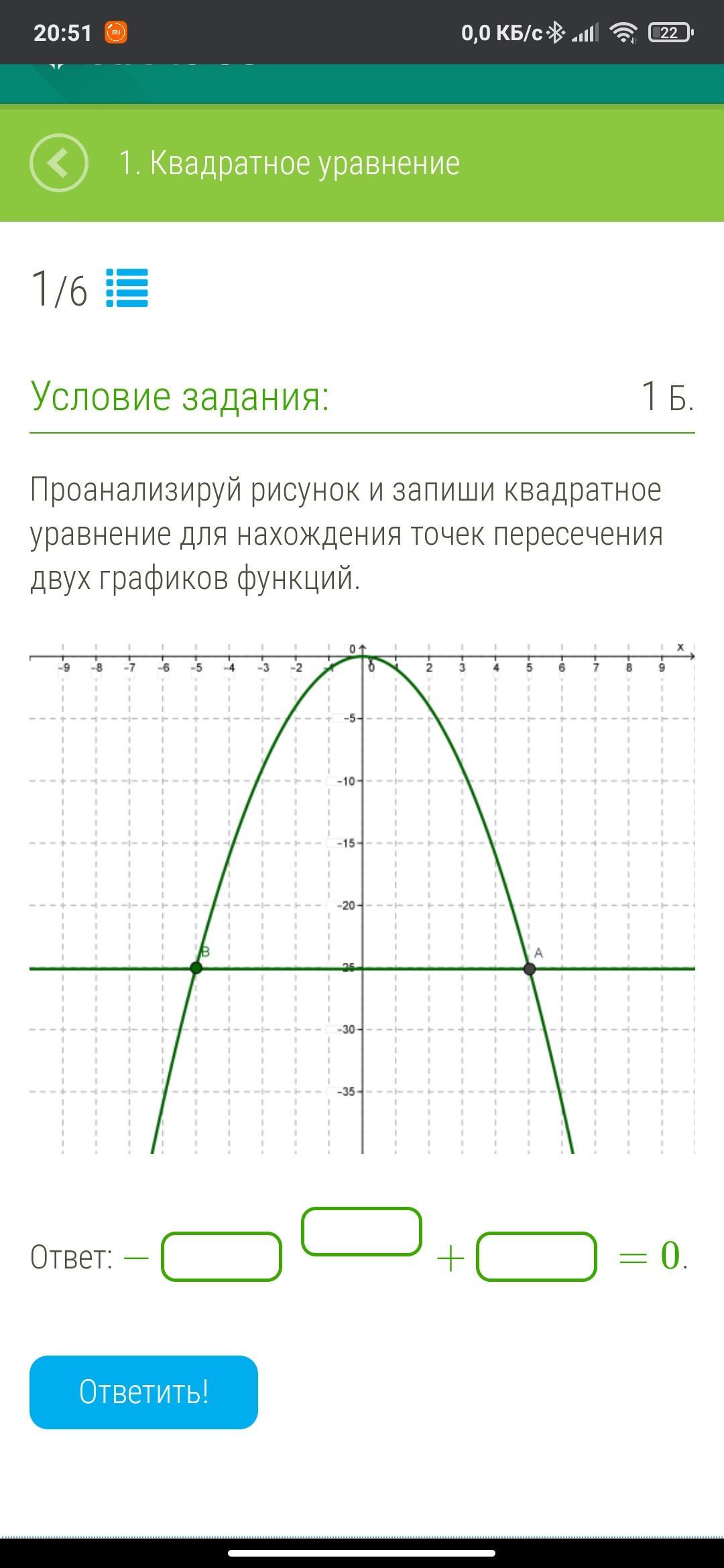
Проанализируй рисунок и запиши квадратное уравнение для нахождения точек пересечения двух графиков функций.
Помогите пожалуйста, желательно с объяснением

Answer 1

На рисунке изображены гафики двух функций:

1-парабола- график квадратичной функции,

2- прямая- график линейной функции.

1- Вершина параболы находится в точке х=0,у=0 (0;0),следовательно ,уравнение функции имеет вид: у= х²

Ветви параболы направлены вниз,следовательно, а < 0.

Отсюда,получаем уравнение данной квадратичной функции:

у = - х²

2- Прямая параллельна оси ОХ и проходит через точку у =-25,следовательно, уравнение данной линейной функции будет иметь вид:

у = - 25

Составим систему данных уравнений и получим квадратное уравнение для нахождения точек пересечения двух графиков функций.

Answer 2

Ответ:

В решении.

Объяснение:

На рисунке два графика: парабола - уравнение у = -х² и прямая, уравнение у = -25.

Почему парабола у = -х²? Потому, что ветви направлены вниз (знак минус перед х²), вершина в начале координат (нет смещения ни по оси Ох, ни по оси Оу), и при значении х=±5  у= -25, х в квадрате.

Приравнять правые части (левые равны):

-х² = - 25

х² = 25

х₁,₂ = ±√25

х₁ = -5

х₂ = 5.

Корни квадратного уравнения являются абсциссами (значениями х) точек пересечения графиков. Ордината (значение у) = -25.

Координаты точек пересечения (-5; -25);  (5; -25).

Квадратное уравнение -х² = - 25 можно записать в виде:

-х² + 25 = 0.