Question

Докажите теорему . В равнобедренном треугольнике
медиана, биссектриса и высота,
проведенные к основанию, совпадают.​

Answer 1

Ответ:

Доказательство теоремы:

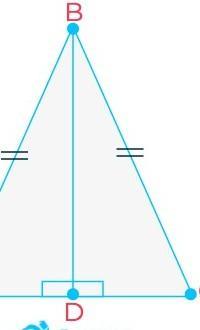
Дан Δ ABC.

Из точки В проведем высоту BD.

Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.к. гипотенузы и общий катет у них равны (теорема Пифагора).

Прямые АС и BD называются перпендикуляром.

В Δ ABD и Δ BCD ∠ BАD = ∠ BСD (из Теоремы 1).

АВ = ВС — боковые стороны равны.

Стороны АD = СD, т.к. точка D отрезок делит пополам.

Следовательно Δ ABD = ΔBCD.

Биссектриса, высота и медиана это один отрезок - BD