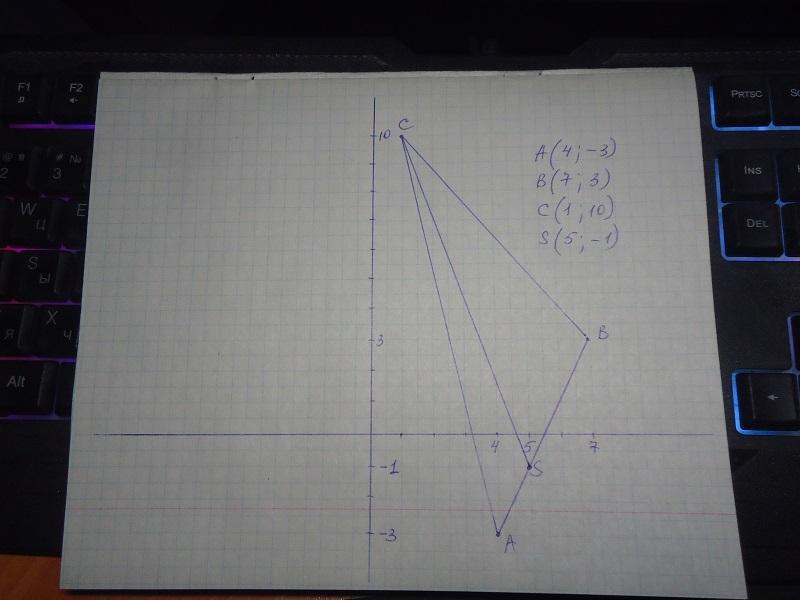
известны координаты вершин треугольника АВС. А(4;-3) В(7;3) С(1;10). Найти уравнение прямой СS, если точка S такая, что BS/SA=2
Ответы
Ответ:
В решении.
Пошаговое объяснение:
Известны координаты вершин треугольника АВС. А(4;-3) В(7;3) С(1;10). Найти уравнение прямой СS, если точка S такая, что BS/SA=2.
1) Построить треугольник АВС по заданным координатам его вершин.
2) Измерить длину стороны АВ. Длина стороны АВ=6,6 см.
3) Дано, что BS/SA = 2, то есть, BS в два раза длиннее SA.
Найти длину BS:
6,6 : 3 * 2 = 4,4 (см).
Отметить точку S на прямой АВ и определить её координаты.
Координаты точки S (5; -1).
4) Найти уравнение прямой СS.
Известны координаты двух точек: С(1; 10) и S(5; -1).
Формула, при помощи которой можно построить уравнение прямой по двум точкам:
(х - х₁)/(х₂ - х₁) = (у - у₁)/(у₂ - у₁)
х₁ = 1 у₁ = 10
х₂ = 5 у₂ = -1
Подставить значения в формулу:
(х - 1)/(5 - 1) = (у - 10)/(-1 - 10)
(х - 1)/4 = (у - 10)/(-11), перемножить, как в пропорции, крест-накрест:
(-11) * (х - 1) = 4 * (у - 10)
-11х + 11 = 4у - 40
-4у = -40 - 11 + 11х
-4у = -51 + 11х
4у = 51 - 11х
у = (51 - 11х)/4
у = 12,75 - 2,75х - искомое уравнение.
Рисунок прилагается.