Предмет: Алгебра,
автор: nuriknematov123321
Продифференцировать функции
Приложения:
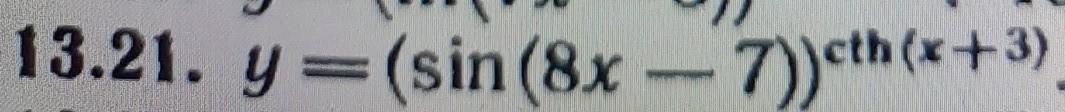
Ответы
Автор ответа:
0
Ответ:
формула:
olga828221:
Hello?
Похожие вопросы
Предмет: Математика,
автор: natalya8684
Предмет: Русский язык,
автор: katya181186
Предмет: Математика,
автор: TyrboKostya
Предмет: Алгебра,
автор: help392
Предмет: Математика,
автор: Анна666111