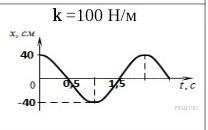
На рисунке показан график гармонического колебания груза, подвешенного к пружине жесткостью 100 Н/м, Определите:
1)период колебаний - Т=
2)частоту колебаний - ν=
3)циклическую частоту - ω=
4)амплитуду колебаний А=
5)записать уравнение гармонического колебания для данного графика
6)записать уравнение скорости гармонического колебания:
7)максимальную скорость - υmax=
8)записать уравнение ускорения гармонического колебания
9)максимальное ускорение amax=
10)массу груза, подвешенного на пружине (любым одним способом)
Ответы
Ответ:
Объяснение:
1)период колебаний - Т= 2 c ( из графика)
2)частоту колебаний - ν= 1/T=0,5 Гц
3)циклическую частоту - ω= 2п/T=п ( с^-1)
4)амплитуду колебаний А= 40 см= 0,4 м
5)записать уравнение гармонического колебания для данного графика X=0,4*cos п*t ( в метрах) в СИ
6)записать уравнение скорости гармонического колебания:
V=X'=-0,4*3,14sin пt=-1,256 sin пt
7)максимальную скорость - υmax= 0,4*3,14=1,256 м/с
8)записать уравнение ускорения гармонического колебания
a=V'=-1,256*3.14*сos пt=-3.944*cos пt
9)максимальное ускорение amax= 3.944 м/с2
10)массу груза, подвешенного на пружине (любым одним способом)
так как k=100 Н/m T= 2п √m/k
T^2= 4 п^2*m/k
m=4*100/4*9.86=10.14 кг
в физике ошибок нет а числа перепроверь !!!!!
Эта - нормальная
и это верный подход ( основная масса ТУПО списывают)
Ответ:
Объяснение:
Т=2 с;
ν=1/T=0.5 Гц;
w=2пv=п или 3.14 рад/с;
А=40 см или 0.4 м
x(t) =Acoswt= 0.4cosπt
υ=-ωΑsinωt=-0.4πsinπt
υmax=ωΑ=0.4π
a=-Aω²cosωt=-0.4π²cosπt
amax=Αω²= 0.4π²
Массу находим через период Т=2π¬/m/k (¬/ — это корень, если не понятно)
Вырази m:
Т²=4π²m/k;
m=T²k/4π²= 4×100/4×10=10 кг
P. S. Если нужно, π переведите сами.