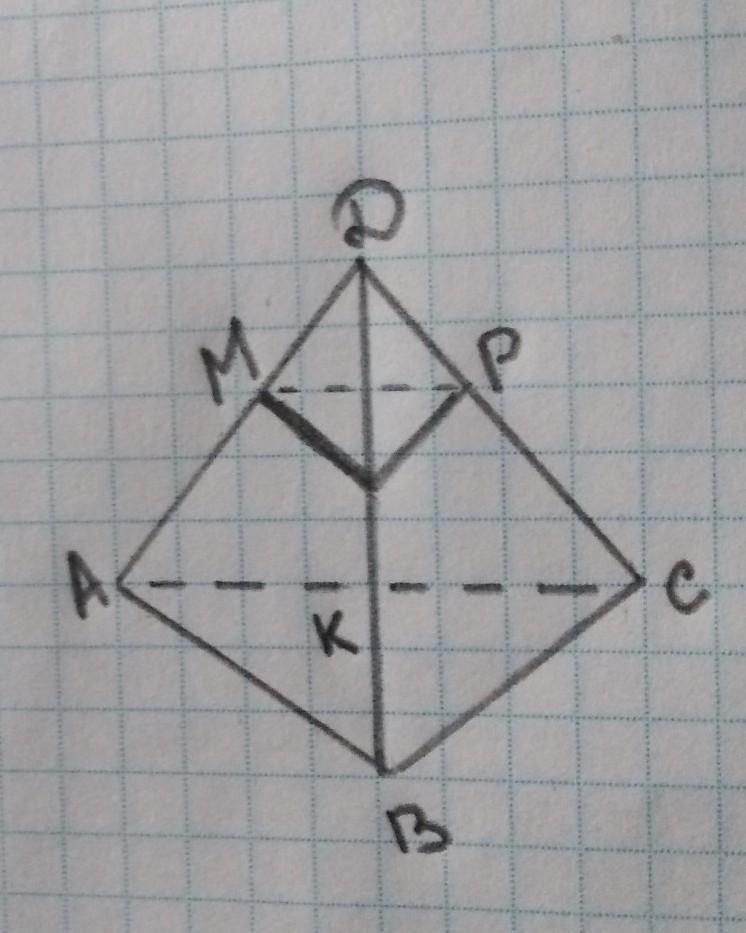
В ТЕТРАЭДЕ АBCD ТОЧКИ M, P, СООТВЕТСТВЕННО СЕРЕДИНЫ РЁБЕР AD, CD, BD УКАЖИТК ВЕРНЫЕ УТВЕРЖДЕНИЯ
А) ПРЯМАЯ МК ПАРАЛЛЕЛЬНАЯ ПЛОСКОСТИ АВС
Б) ПРЯМЫЕ МD И ВС СКРЕЩИВАЮЩИЕСЯ
В) ПЛОСКОСТЬ MPK ПАРАЛЛЕЛЬНА ПЛОСКОСТИ BCD
Ответы
А) ПРЯМАЯ МК ПАРАЛЛЕЛЬНАЯ ПЛОСКОСТИ АВС - верно.
Признак параллельности прямой и плоскости: Если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельно данной плоскости. Рассмотрим треугольник АВД. М и К середины сторон, значит МК - средняя линяя. Средняя линия треугольника параллельна основанию, т.е. МК||АВ. АВ лежит в плоскости АВС. Отсюда следует, что МК|| (АВС)
Б) ПРЯМЫЕ МD И ВС СКРЕЩИВАЮЩИЕСЯ - верно
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся. Рассмотрим плоскость АВС. ВС лежит в этой плоскости. МД пересекает эту плоскость в точке А, не принадлежащей ВС. Значит МД и ВС скрещиваются.
В) ПЛОСКОСТЬ MPK ПАРАЛЛЕЛЬНА ПЛОСКОСТИ BCD - неверно
Две плоскости называются параллельными, если они не имеют общих точек.
Плоскости МКР и ВСД пересекаются по прямой КР, значит они не могут быть параллельны
Ответ: АБ