Предмет: Математика,
автор: cris2020
Помогите найти: для функции z = f(x,y) найти градиент и производную по направлению a ̅ в точке A.
Приложения:
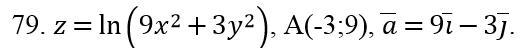
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
градиент функции z = f(x,y) это вектор, координатами которого являются частные производные данной функции.
частные производные
теперь в точке А(-3;9)
теперь направление
направление вектора-градиента задаётся его направляющими косинусами
ищем модуль градиента в точке А
теперь производная в точке А по направлению вектора а(9;-3).
и вот
и поскольку dz/da < 0, то заданная функция в направлении вектора a убывает.
Похожие вопросы
Предмет: Математика,
автор: jasigafurova1
Предмет: Биология,
автор: секр
Предмет: Английский язык,
автор: katyakosheleva3
Предмет: Геометрия,
автор: Masha110502