Предмет: Геометрия,
автор: ramirkaramitka
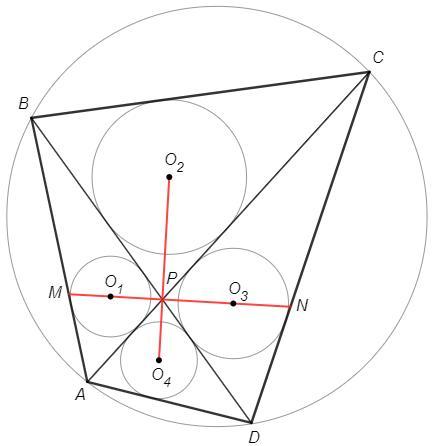
35б. Помогите! Диагонали выпуклого четырѐхугольника ABCD пересекаются в точке
P. В треугольники APB, BPC, CPD и APD вписаны окружности с центрами O1,
O2, O3 и O4 соответственно.
а) Докажите, что прямые O1O3 и O2O4 перпендикулярны.
б) Пусть прямая O1O3 пересекает стороны AB и CD в точках M и N
соответственно. Найдите отношение площадей треугольников CPN и DPN, если
около четырѐхугольника ABCD можно описать окружность и AM : MB = 1 : 2.
ramirkaramitka:
Хотя бы только под одной буквой
чтобы вы просто списали? чтобы решать такие задачи, надо хоть что-то понимать в геометрии, у вас же решений на сайте-вообще никаких...
Ответы
Автор ответа:
1
a) Центры вписанных окружностей лежат на биссектрисах.
Биссектрисы вертикальных углов составляют прямую.
Биссектрисы смежных углов перпендикулярны.
PO1⊥PO2 => O1O3⊥O2O4
б) ∠BAC=∠BDC (вписанные углы), △APB~△DPC (по углам)
Биссектрисы PM и PN являются соответствующими отрезками в подобных треугольниках => делят соответствующие стороны в равном отношении.
DN/NC =AM/MB =1/2
Площади треугольников с равными высотам относятся как основания.
S(CPN)/S(DPN) =NC/DN =2/1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: nlo1
Предмет: Алгебра,
автор: amirratmir
Предмет: Математика,
автор: ФяФяЯф
Предмет: Математика,
автор: Mansur12351