Question

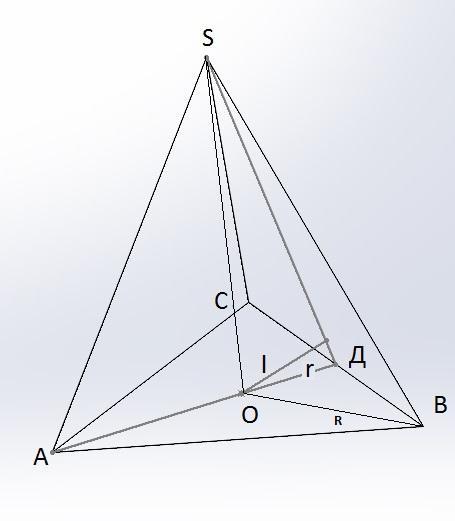
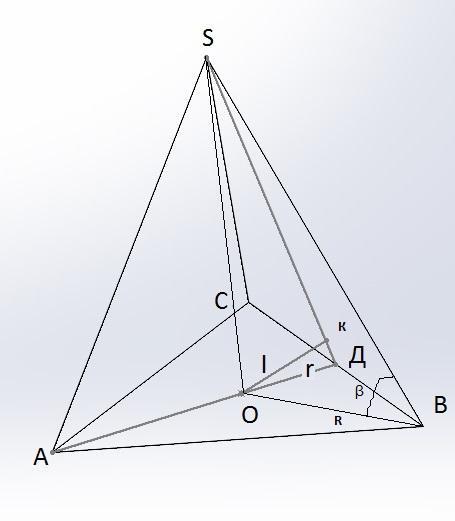
перпендикуляр, опушенный из центроида основания правильной треугольной пирамиды на боковую грань равен l, найти обьем пирамиды если угол между боковым ребром и плоскостью основания равен бетта.

Answer 1

Ответ:

V=1/3*SΔABC*OS = 1/3*12l^2(4tg^2β+1)/2tgβ)$\sqrt{3}$/4*2r*tgβ

SΔABC = 12r^2$\sqrt{3}$/4    r =l($\sqrt{(4tg^2\beta+1 )/2tg\beta }$

Из подобных ΔОДS и ΔОДК определяем ДS =r*ОS/l

ОS=R*tgβ = 2r*tgβ   ДS =2r^2*tgβ/l

Объяснение: