Предмет: Математика,
автор: aliciakey
Математика. 1 курс. Помогите пожалуйста
Приложения:

CheckmateTheKing:
Удачи, я в 10, что же меня ждёт...
да ничего страшного нет. писанины только много.. -))
Ну я неумный
тут ума не много надо. просто помнить какую формулу куда пристроить ... )))))
Спасибо за разъяснение, теперь буду не так бояться)
образайтесь, если понадобится помощь -)))))
Ответы
Автор ответа:
3
Ответ:
Пошаговое объяснение:
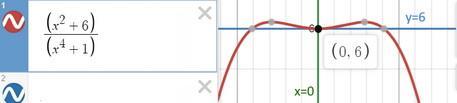
1)
x₀ = 0
уравнение касательной
y(0)= 6
тогда
и уравнение касательной будет иметь вид
теперь нормаль
если производная в точке x₀ равна нулю то касательная параллельна оси Ox (что у нас и есть) а уравнение нормали имеет вид x = x₀
т.е. наше уравнение нормали
х = 0
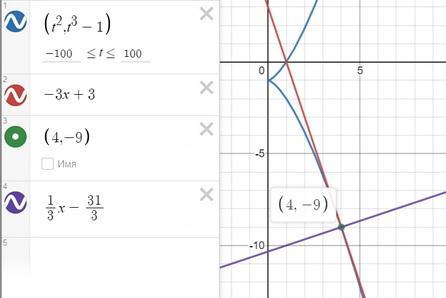
2)
t₀= -2
найдем точку, соответствующую параметру t₀= -2
x₀(-2) = 4; y₀(-2) = -9 ⇒ M(x₀; y₀) =M(4; -9)
уравнения касательной в общем виде
так как функция задана в параметрическом виде, то отдельно находим производные и
подставим в уравнение в общем виде
или
нормаль
(x-4)*(-4)+(y+9)*12=0
Приложения:
спасибо огромное <3
Похожие вопросы
Предмет: Қазақ тiлi,
автор: kalashnovd
Предмет: Математика,
автор: Medinanasaeva
Предмет: Русский язык,
автор: aydan2002
Предмет: Математика,
автор: oks1995
Предмет: Математика,
автор: ilchenkoirochka