Предмет: Математика,
автор: yavoitov2017
Отдаю все баллы, помогите пожалуйста.
Приложения:
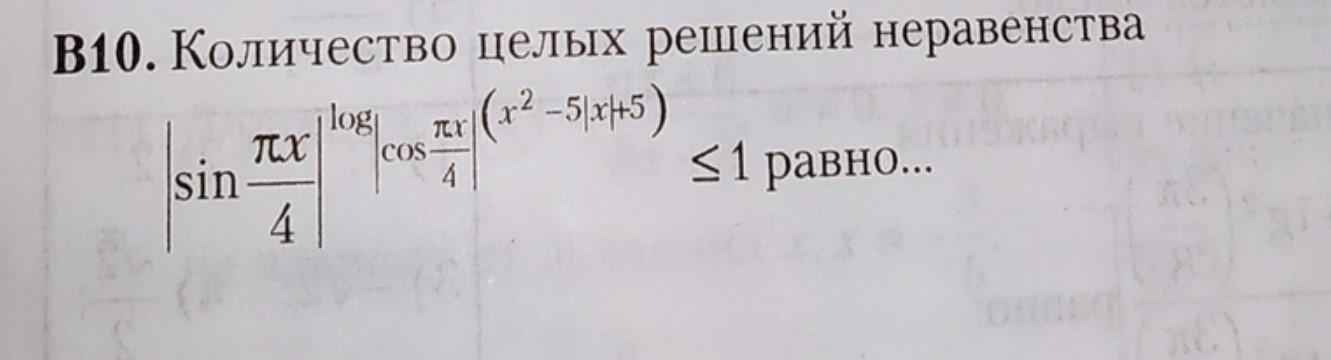
afanasevatamara77:
прости я ещё только в 5 классе и этого не проходила
Ответы
Автор ответа:
2
ОДЗ:
и
Рассмотрим ОДЗ подробнее:
если , то ввиду тождества:
имеем .
И если , то исходя из того же тождества, имеем
Это значит
, k∈Z,
.
, m∈Z,
.
Итак, ОДЗ:
, k∈Z,
, m∈Z,
Теперь решаем само уравнение:
Т.к. , то функция
убывающая и поэтому имеем
Т.к. , то функция
убывающая, поэтому имеем
Мы ищем только целочисленные решения, тогда:
x может принимать значения:
-1; -2; -3; -4; 1; 2; 3; 4. Из них в ОДЗ входят лишь: -1 и 1.
Ответ. Два целочисленных решения.
С Новым годом Вас!
Спасибо, вас также
Похожие вопросы
Предмет: Английский язык,
автор: arubikelike
Предмет: Другие предметы,
автор: viktoriabak10
Предмет: Математика,
автор: петро0читель
Предмет: Математика,
автор: ЛизаПерунова
Предмет: Биология,
автор: Maksima9898