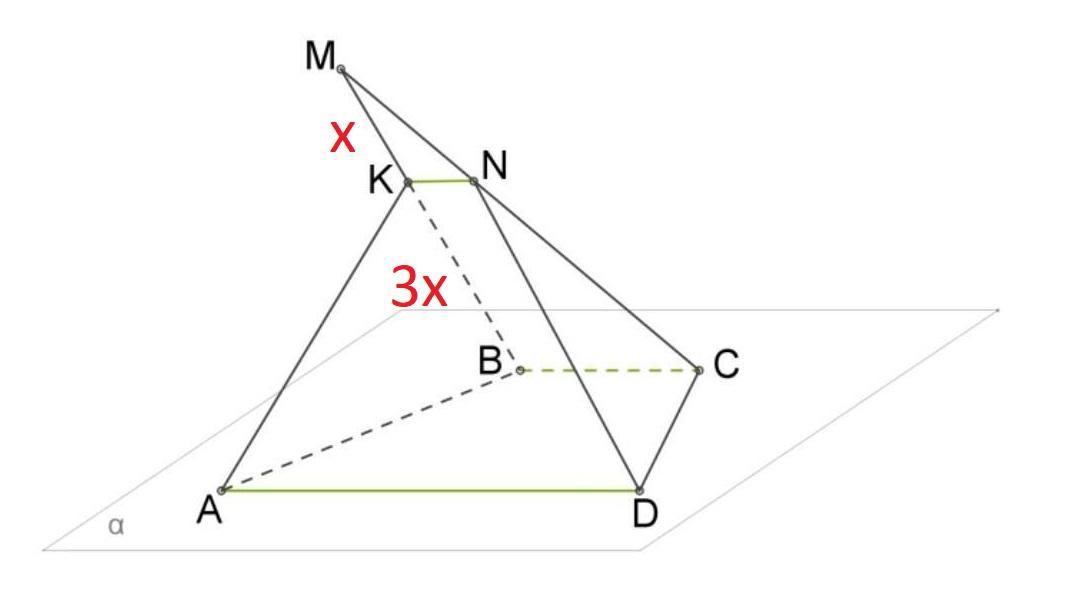
Трапеция ABCD, основание BC которой равно 24 cм, лежит в плоскости α. Точка M не находится в плоскости трапеции. Точка K делит отрезок MB так, что MK:KB=1:3. Плоскость ADK пересекает отрезок MC в некоторой точке N. Определи длину отрезка KN.
1. Назови пучок параллельных прямых (достаточно ввести одну прямую в каждое окошко, буквы располагай в алфавитном порядке!):
∥
∥
.
2. Назови подобные треугольники:
ΔKMN~Δ
.
3. KN=
(округли до одной десятой).
Предыдущее задание
Предыдущее задание
Список заданий
Список заданий
Следующее задание
Следующее задание
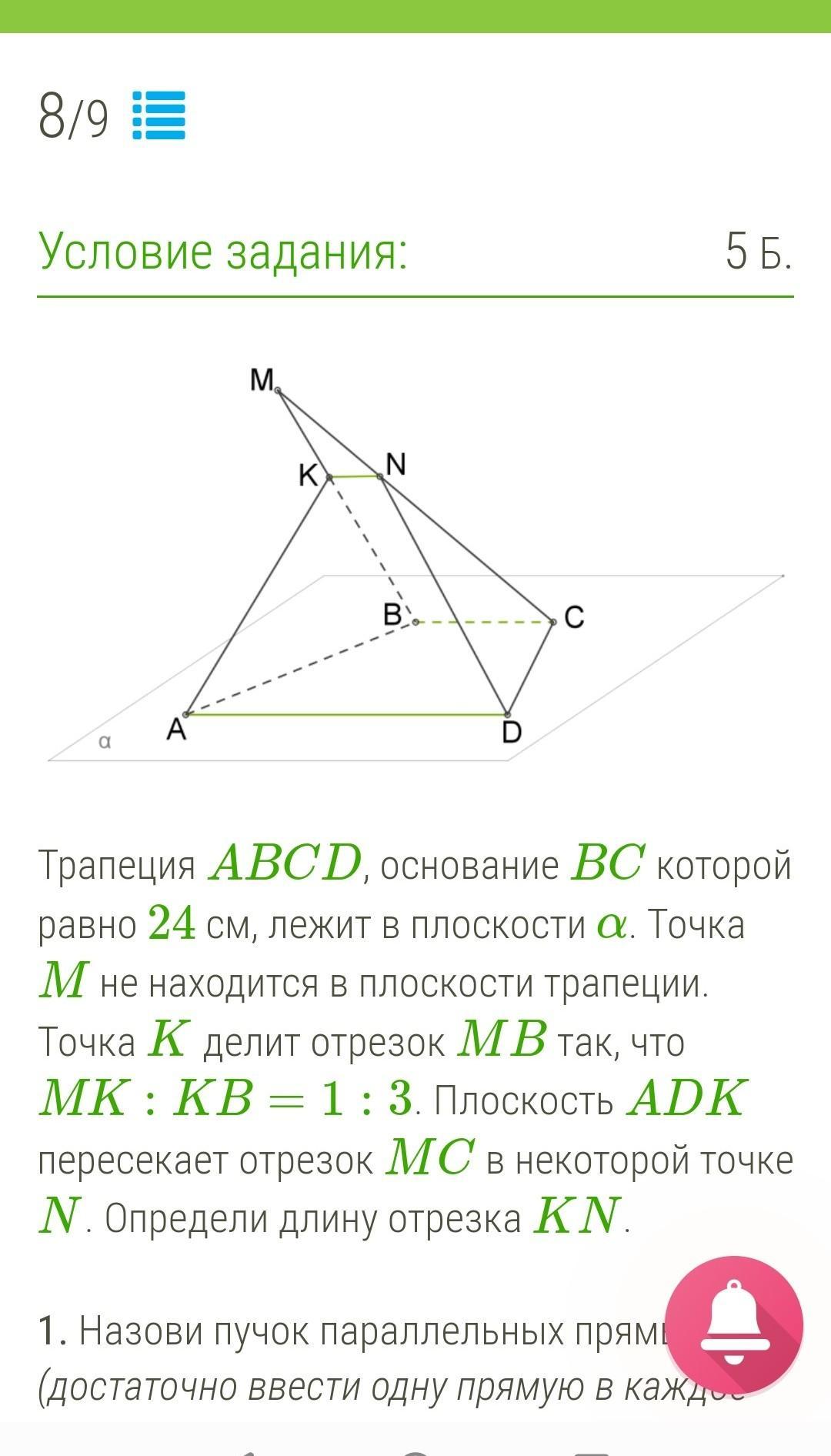
ΔKMN~Δ
Ответы
Ответ:
KN = 6 см
Объяснение:
Дано: ABCD - трапеция, BC = 24 см, BC║AD, M ∉ α; A,B,C,D ∈ α;
MK : KB = 1 : 3, ADK ∩ MC = N
Найти: KN - ?
Решение: Плоскость AKN ∩ BKN = KN, так как K,N ∈ BKN и K,N ∈ AKN. По теореме если через каждую из двух параллельных прямых проведена плоскость, при этом эти плоскости пересекаются по прямой, отличной от двух данных, то эта прямая параллельна каждой из двух прямых, так как AKN ∩ BKN = KN и по условию BC║AD, то BC║AD║KN. Рассмотрим треугольник ΔBMC. Так как BC║KN, то
угол ∠MKN = ∠MBC, ∠MNK = ∠MCB как соответственные углы при параллельных прямых по теореме и угол ∠BMC - общий для треугольников ΔMKN и ΔMBC, то треугольник ΔMKN подобен треугольнику ΔMBC по первому признаку подобия треугольников. Введем коэффициент пропорциональности x,
тогда MK = x, KB = 3x.
MB = MK + KB = x + 3x = 4x. Так как треугольник ΔMKN подобен треугольнику ΔMBC, то по свойствам подобных треугольников: см.