Предмет: Алгебра,
автор: rabbitti
Срочно помогите пожалуйста
Приложения:

Ответы
Автор ответа:
1
Ответ:
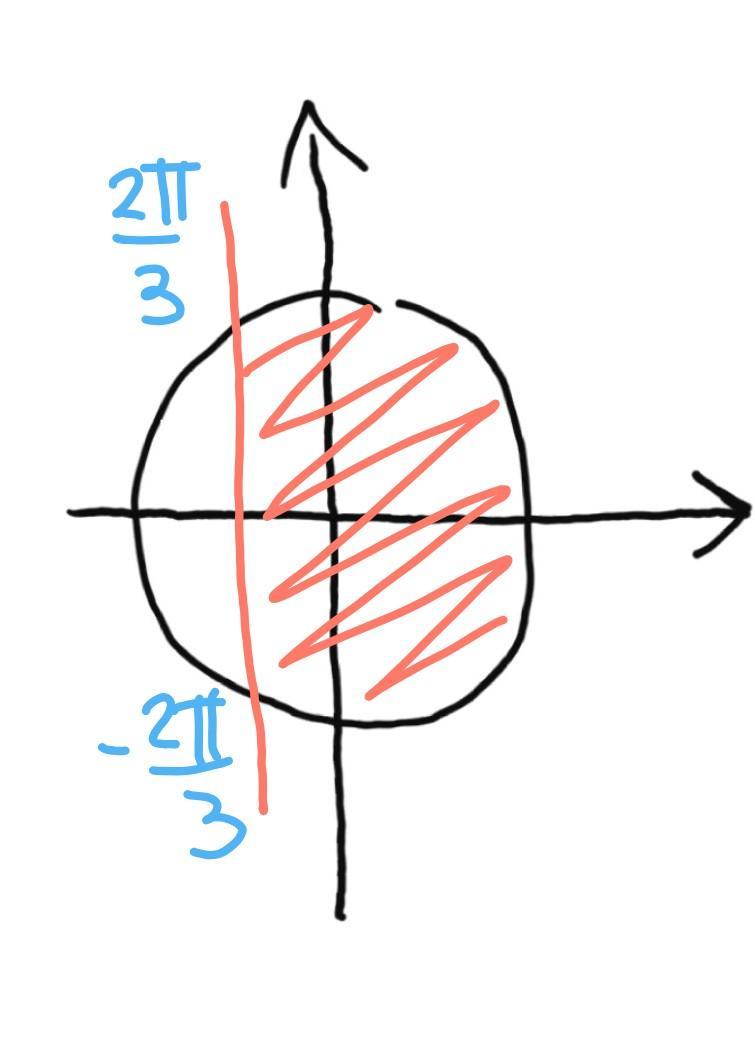
1.
рисунок
n принадлежит Z.
2.
Приложения:
rabbitti:
можете чекнуть вопрос про вероятность??
Автор ответа:
1
Ответ:
решение на фото.........
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Tora11
Предмет: Русский язык,
автор: Iazik
Предмет: Математика,
автор: 1478529630000
Предмет: Физика,
автор: Владочка0212
Предмет: Алгебра,
автор: lerakkkkkk