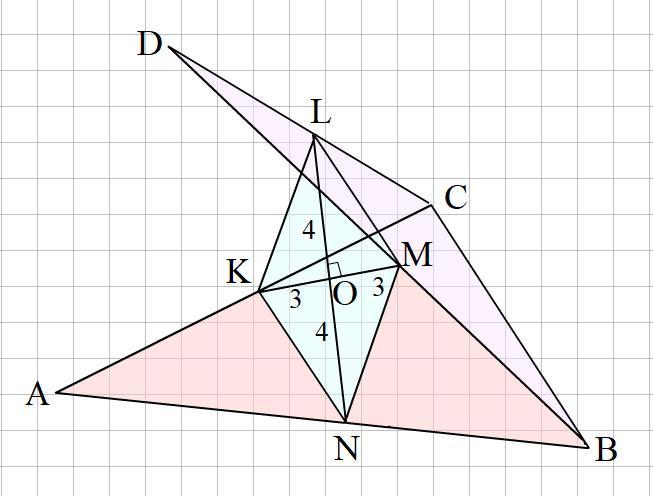
Точки A, B, C, D не лежать в одній площині; точки K, L, M, N — середини відрізків AC, CD,BD, AB відповідно, AD=BC . Знайдіть периметр чотирикутника KLMN, якщо KM=6 см, NL=8см.
Ответы
Ответ:
Периметр KLMN равен 20 см
Объяснение:
Поскольку точки A, B, C, D не лежат в одной плоскости, то это значит, что три точки А, В, С, образуют плоскость а точка D ∉ плоскости АВС.
Изобразим это на рисунке (смотри прикреплённый рисунок)
Соединим отрезками точки А и С, точки С и D, точки В и D, точки А и В и нанесём срединные точки этих отрезков K, L, M, N.
По рисунку:
В Δ BDC средняя линия LM || BC и равна LM = 0.5 BC.
В Δ ABC средняя линия KN || BC и равна KN = 0.5 BC.
Поскольку LM || BC и KN || BC, то LM || KN.
Если в четырёхугольнике KLMN противоположные стороны LM и KN равны и параллельны, то этот четырёхугольник - параллелограмм.
Аналогично:
В Δ ABD средняя линия MN || AD и равна MN = 0.5 AD.
В Δ ADC средняя линия KL || AD и равна KL = 0.5 AD.
Следовательно,
KL = MN = 0,5 АD
По условию AD = BC, поэтому все стороны параллелограмма равны между собой LM = KN = LM = KL, и параллелограмм KLMN является ромбом.
КM и NL являются диагоналями ромба KLMN, следовательно, КM ⊥ NL.
Диагонали ромба делятся точкой пересечения пополам, поэтому
КО = 0,5 КМ = 3 см
LO = 0.5 NL = 4 cм
и сторона ромба по теореме Пифагора
KL² = LO² + КО²
KL² = 4² + 3² = 25
KL = 5 (см)
Периметр ромба KLMN равен
Р = 4 KL = 4 · 5 = 20 (cм)