Предмет: Алгебра,
автор: nuriknematov123321
продифференцировать функции
Приложения:
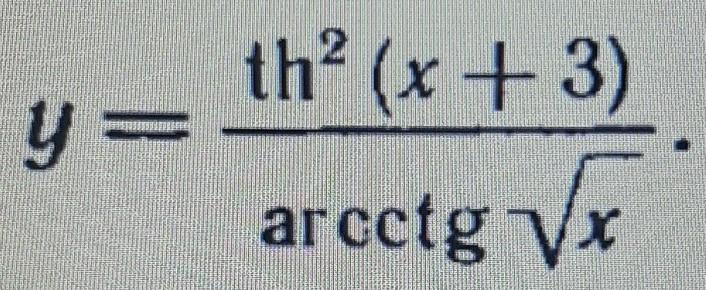
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: КотУчёныйМяу
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: История,
автор: Lhsim
Предмет: Математика,
автор: pechenkav8
Предмет: История,
автор: Аноним