Предмет: Математика,
автор: veronika17038oe
Помогите решить предел
Приложения:
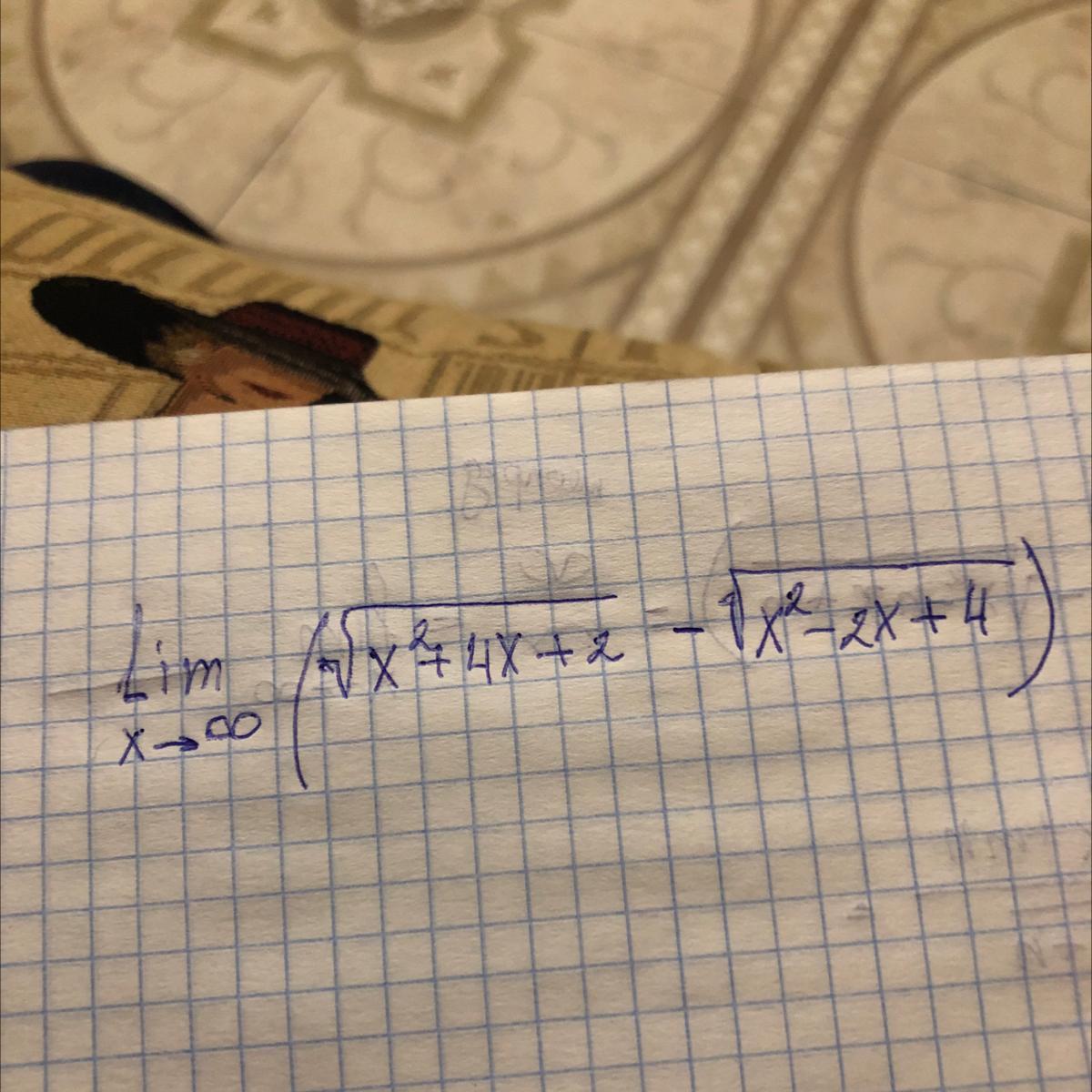
veronika17038oe:
Вк
если не сложно
Ответы
Автор ответа:
1
А почему половина решения обрезано?
Думал, что только у меня. Понятия не имею - проблема сайта)
но в любом случае спасибо
Автор ответа:
1
----------------------------
Приложения:
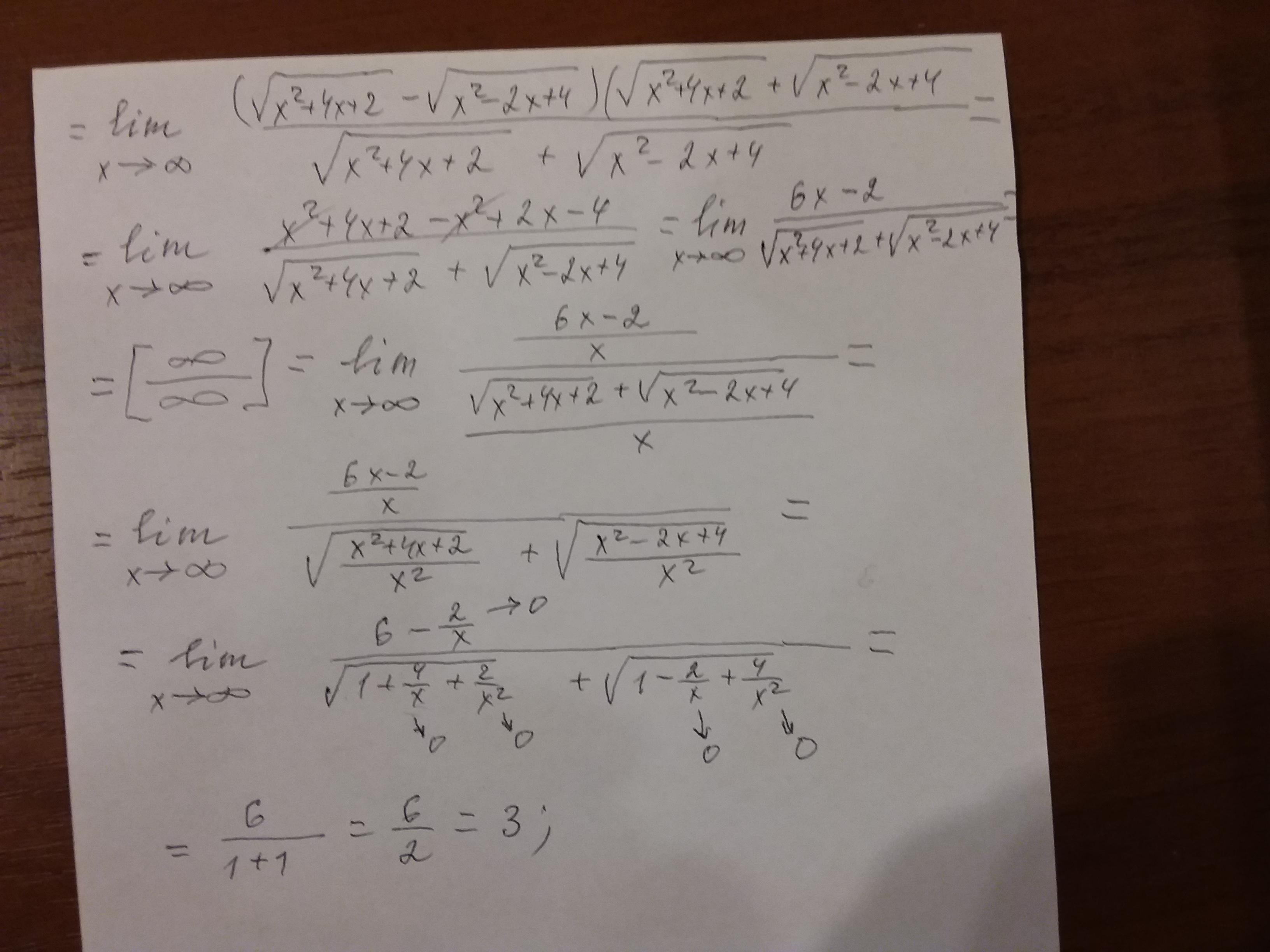
Скобочку забыли в первой строке в самом конце ^_^
Похожие вопросы
Предмет: Русский язык,
автор: ДёминаЛиза
Предмет: Физика,
автор: deimone1
Предмет: Русский язык,
автор: SофьяKаганюк
Предмет: Математика,
автор: masha1291