Предмет: Математика,
автор: ZPeHNe
Помогите решить интеграл
Приложения:
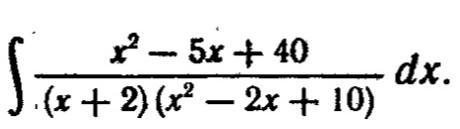
ZPeHNe:
Ну очень срочно нужно, памагити
Ответы
Автор ответа:
0
Ответ:
С помощью неопределенных коэффициентов (раскладываем на простейшие дроби):
Получаем:
1 интеграл
2 интеграл
Объединяем. Ответ:
Похожие вопросы
Предмет: Математика,
автор: Minikotik12
Предмет: Английский язык,
автор: вадим90
Предмет: История,
автор: vlad03jove
Предмет: География,
автор: kamilla476
Предмет: Алгебра,
автор: arxanisaev