Предмет: Математика,
автор: pandoratvset
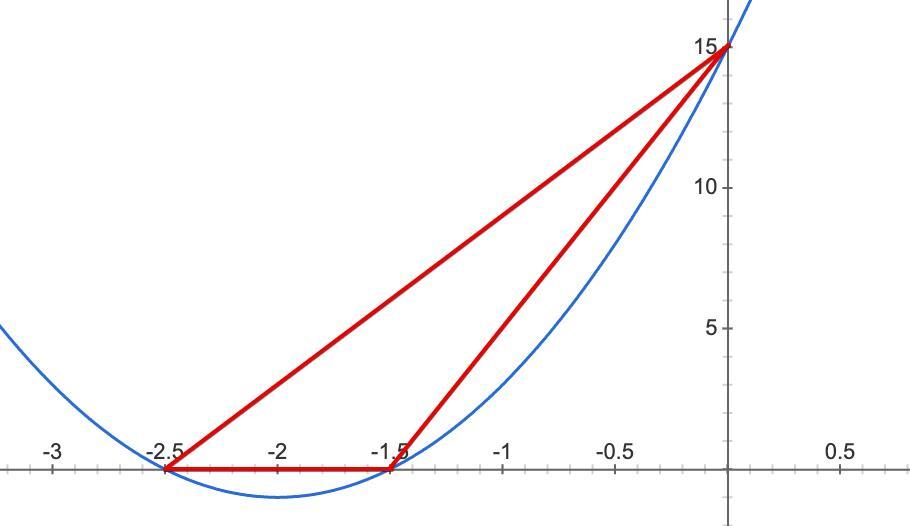
квадратичная функция задается формулой y=4x^2+16x+15.Найдите площадь треугольника,вершинами которого является точки пересечения графика функции с осями координат
Ответы
Автор ответа:
0
Ответ:
7,5 ед^2
Пошаговое объяснение:
Для определения точек пересечения графика с осями координат необходимо решить уравнение относительно y при x = 0 (пересечение с осью OY) и относительно x при y = 0 (пересечение с осью OX).
1) Пересечение с осью OY, x = 0
2) Пересечение с осью OX, y = 0
Будем считать, что основание треугольника лежит на оси абсцисс, тогда:
где a -- длина основания, h -- длина высоты, S -- площадь треугольника.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: azam291
Предмет: Химия,
автор: Танюша2002841
Предмет: Қазақ тiлi,
автор: dan228228
Предмет: Алгебра,
автор: Sanunsysanin228
Предмет: Математика,
автор: romadodonovz