Предмет: Алгебра,
автор: aab0810
блин решите задачу по алгебре 11 класс , не могу решить помогите :(
Приложения:
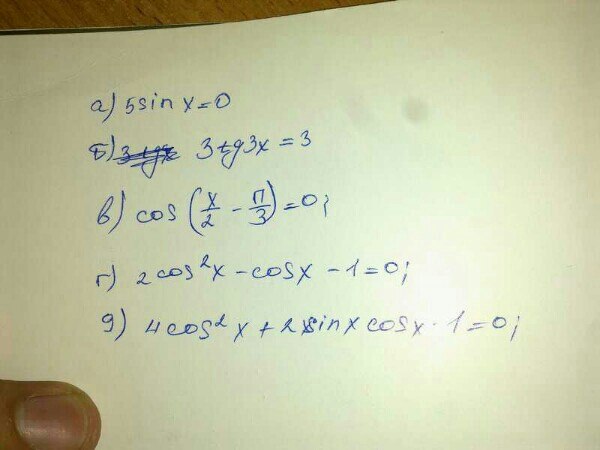
Ответы
Автор ответа:
0
1. 




Ответ:
2.




ответ:
3.











ответ: ;
; 
4.
Пусть , тогда уравнение примет вид:
, тогда уравнение примет вид:




откуда:







Ответ: ;
; 
Ответ:
2.
ответ:
3.
ответ:
4.
Пусть
откуда:
Ответ:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: pp4454texno
Предмет: Окружающий мир,
автор: Аноним
Предмет: Физика,
автор: moarmytiny
Предмет: Физика,
автор: alinagaitsyk
Предмет: Математика,
автор: z1982