Предмет: Геометрия,
автор: vitaliok777
СРОЧНО ПОМОГИТЕ
Сломал руку. Теперь не понимаю
Приложения:
vitaliok777:
Умоляю Помогите
Ответы
Автор ответа:
4
Ответ:
(см. объяснение)
Объяснение:
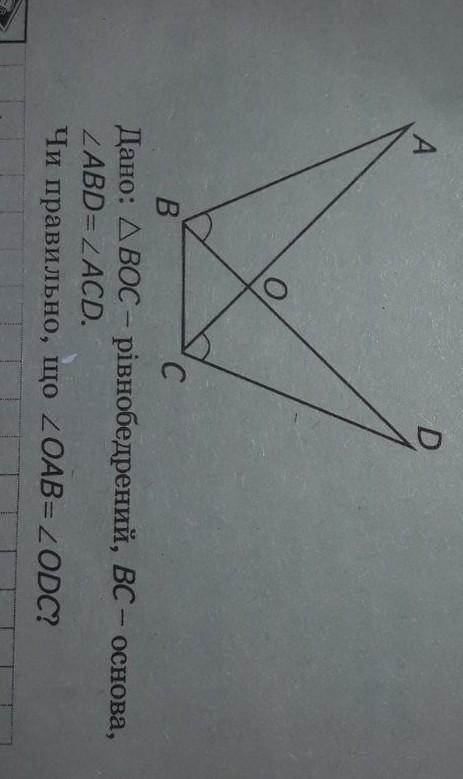
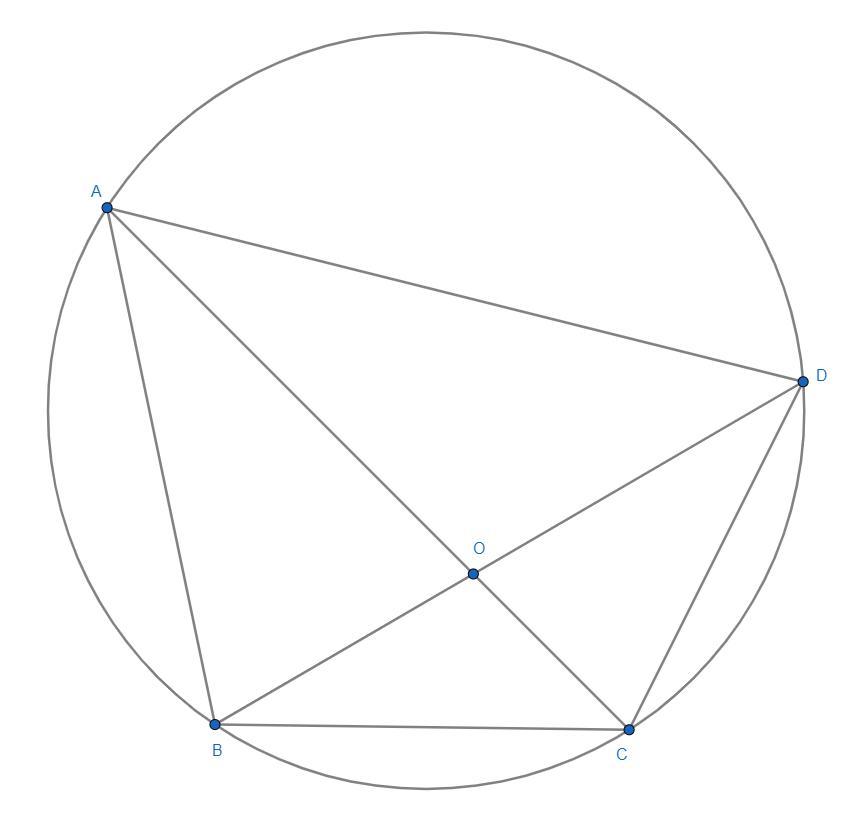
Так как ∠ABD=∠ACD и эти углы опираются на сторону AD, то существует такая окружность, в которой ∠ABD и ∠ACD являются вписанными, опирающимися на дугу AD. Тогда точки A, B, C и D лежат на одной окружности. Иными словами, четырехугольник ABCD вписанный. Обратим теперь внимание на то, что ∠CAB=∠BDC, так как это вписанные углы, опирающиеся на дугу BC. Таким образом, мы доказали, что ∠CAB=∠BDC (или ∠OAB=∠ODC).
Доказано!
Комментарий:
Замечу, что равнобедренность треугольника вовсе необязательна, то есть условие задачи избыточно. Предполагаю, что составитель хотел, чтобы были рассмотрены треугольники BAO и ODC, которые равны по второму признаку. Тогда из равенства также следует, что ∠OAB=∠ODC.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: safiullin2
Предмет: Русский язык,
автор: malyuzhenko88
Предмет: Математика,
автор: никитаттт
Предмет: Алгебра,
автор: lantanml
Предмет: Математика,
автор: milabulg