Предмет: Математика,
автор: chelovekliveiknow
Прошу помочь, вообще ничего не понимаю...
Найти числовой ряд на сходимость
Приложения:
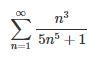
chelovekliveiknow:
Исследовать числовой ряд на сходимость
(на укр) Дослідити числовий ряд на збіжність
Ответы
Автор ответа:
1
Відповідь:
ряд збігається
Покрокове пояснення:
Знайдемо границю n+1 члена ряду до n-го при n→бескінечності
(n+1)^3/(5(n+1)^5+1) : n^3/(5n^5+1) = n^3(1+1/n)^3 / (n^5(5(1+1/n)^5+1/(n^5) × n^5(5+1/n)/(n^3)=
=(1+1/n)^3 / ((5(1+1/n)^5+1/(n^5) × (5+1/n)/1
При n→бесконечности а_(n+1)/a_n→1/(5^5)×5/1=1/(5^4)=
=1/625=0,0016<1. то ряд збігається
Автор ответа:
1
Ответ:
Пошаговое объяснение:
используем признак сравнения
рассмотрим предел общего члена
упростим его
тогда исходный ряд можно представить в виде
а это обобщенный гармонический ряд с α > 1
тогда и исходный ряд сходится.
Похожие вопросы
Предмет: Русский язык,
автор: altctrl23
Предмет: Литература,
автор: a89811400215
Предмет: Другие предметы,
автор: mazuric2008
Предмет: Математика,
автор: варя401
Предмет: Математика,
автор: MasterTVforYouTude