Предмет: Геометрия,
автор: rejx1901
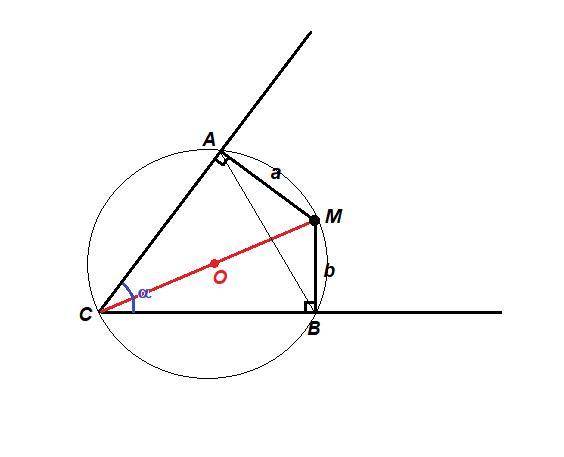
Точка М лежит внутри угла, равного α , на расстоянии a и b от сторон этого угла. Определите расстояние от точки М до вершины угла.
Ответы
Автор ответа:
4
Ответ:
Объяснение:
МА⊥АС, МВ⊥ВС,
МА = а, МВ = b.
В четырехугольнике CAMB сумма противолежащих углов А и В равна 180°, значит вокруг него можно описать окружность.
Эта окружность описана и около прямоугольных треугольников МАС и МВС, значит ее центр О лежит на середине гипотенузы МС.
∠С + ∠М = 180° (свойство вписанного четырехугольника),
∠М = 180° - ∠С = 180° - α
cos ∠M = cos (180° - α) = - cos α
Из ΔАМВ по теореме косинусов:
AB² = MA² + MB² - 2·MA·MB·cos∠M
AB² = a² + b² + 2ab·cosα
По следствию из теоремы синусов для треугольника АВС:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: iuytr566
Предмет: Математика,
автор: nastyha2004
Предмет: Математика,
автор: АселяОкей
Предмет: География,
автор: Ма4ия5