Предмет: Геометрия,
автор: nastyaguliaeva06
помогите пожалуйста срочно
Приложения:
Ответы
Автор ответа:
0
Ответ:
квадратных единиц.
Объяснение:
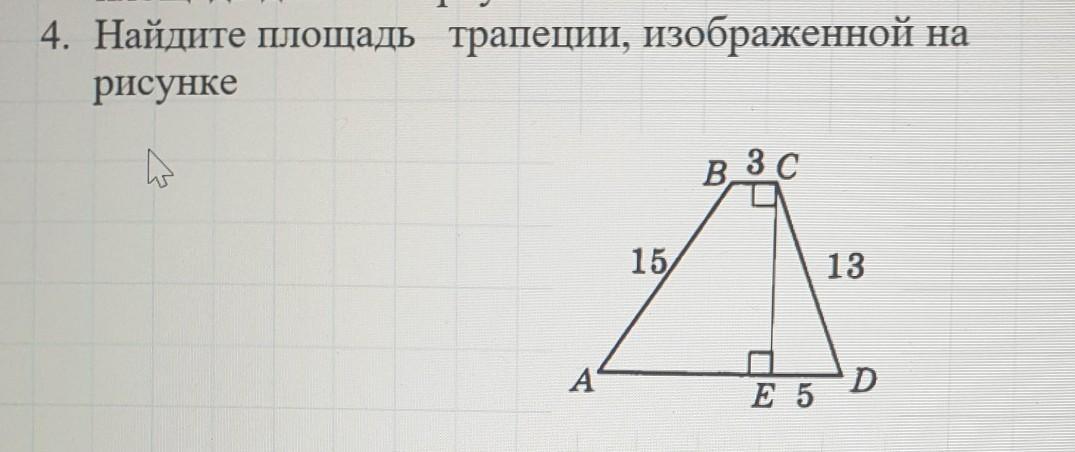
Рассмотрим треугольник ΔCED.Треугольник CED - прямоугольный так как по условию, CE ⊥ AD, тогда по теореме Пифагора:
.
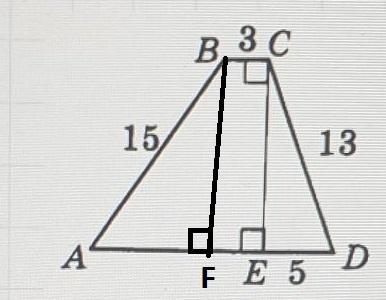
Проведем высоту B из точки на основание AD в точку F.По свойству трапеции все высоты проведенные между основаниями равны, тогда
BF = CE = 12.Треугольник ΔBFA - прямоугольный так как BF ⊥ AD.По теореме Пифагора
Четырехугольник BFEC - параллелограмм, так как по теореме-признаку BF = FE и так как BF ⊥ AD , CE ⊥ AD ⇒ BF ║ CE, тогда четырехугольник BFEC - параллелограмм, по свойству параллелограмма его противоположные стороны равны следовательно BC = FE = 3. AD = AF + +FE + ED = 9 + 3 + 5 = 17.По формуле площади трапеции квадратных единиц.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: lilo26
Предмет: Алгебра,
автор: Настик13
Предмет: Математика,
автор: красныйяр
Предмет: Математика,
автор: 50528200512