Question

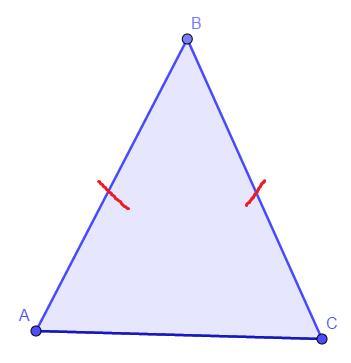
Вказати вид трикутника, якщо AB = 6м; CB = 6м; AC = 10м.​

Answer 1

Ответ:

Трикутник ΔABC - рівнобедренний тупокутний трикутник.

Объяснение:

Так як за умовою AB = 6м,CB = 6м ⇒AB = CB = 6м, отже трикутник є рівнобедренним. За теоремою косинусів:

$AC^{2} = AB^{2} + BC^{2} - 2AB * BC *cos$ ∠ABC

cos ∠ABC = $\frac{AB^{2} + BC^{2} - AC^{2}}{2AB *BC}= \frac{36 + 36 - 100}{2 * 6 * 6}=\frac{72-100}{72} =\frac{-28}{72}= -\frac{7}{18}$ ≈ -0,38

Отже cos ∠ABC < 0, тоді ∠ABC > 90°.

Отже трикутник ΔABC - рівнобедренний тупокутний трикутник.