Предмет: Алгебра,
автор: Torontoo
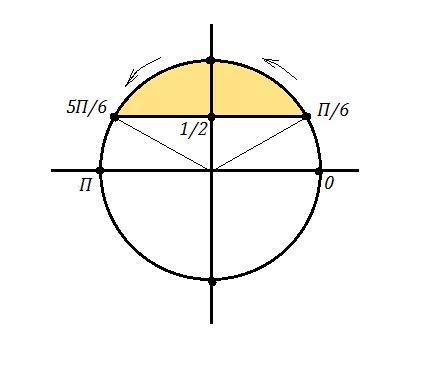
Решите неравенство: 2sin^2x+sinx-1 > 0
Ответы
Автор ответа:
1
Ответ:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Баксёрша
Предмет: История,
автор: Ангелидрау
Предмет: Русский язык,
автор: kznshilova
Предмет: Математика,
автор: staaaasya
Предмет: Математика,
автор: maxglebov777