Question

Докажите , что выражение х²+6х+20 принимает положительное значение при всех значениях х. Какое наименьшее значение принимает это выражение и при каком х?​

Answer 1

Фактически, мы можем сказать, что данный график - это парабола, ветки которой направленны вверх. Вершина параболы - это точка наименьшего значения уравнения, ее можно найти по данной формуле:

$y_{0} = \frac{-b}{2a}=\frac{-6}{2} = -3$ (наименьшее значение выражения)

Подставив это значение, мы получим x₀ координату:

$x_{0} = (-3)^2 - 18 + 20 = 9 + 2 = 11$ (значение переменной x, при самом наименьшем значении)

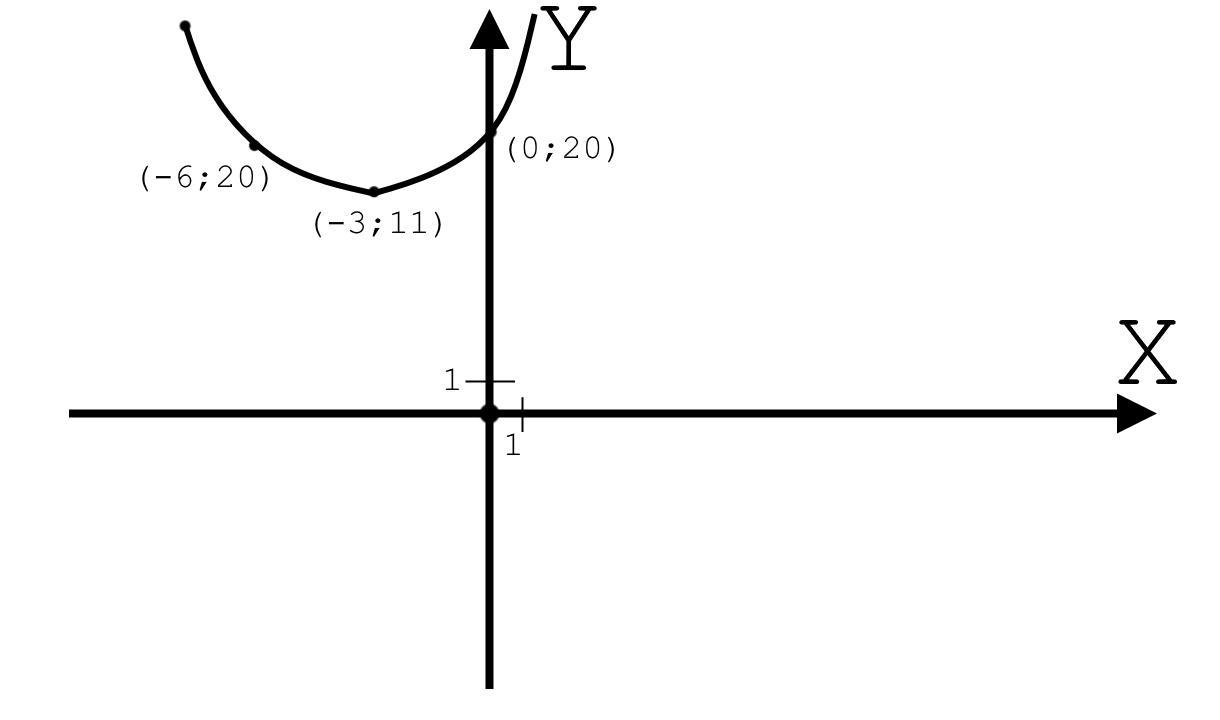
Для того, что бы доказать то, что значения всегда положительны достаточно построить график:

Мы уже знаем координаты вершины, потому нам следует всего лишь найти точку пересечения с осью ординат, подставив в уравнение вместо x, значения 0:

$x = 0, y = (0)^2 + 0 + 20 = 20$

По аналогии, зная что данный график - это парабола можно подставить точку "-6"

$x = -6, y = (-6)^2-36 + 20 = 36 - 36 + 20 = 20$

Имея эти две точки мы можем построить график (прикреплённый файл).

По графику видно, что значения "y" - всегда положительны