Предмет: Математика,
автор: MikiRain
ОЧЕНЬ СРОЧНО ПОМОГИТЕ.Нужно найти общий интеграл дифференциального уравнения 1 порядка
Приложения:
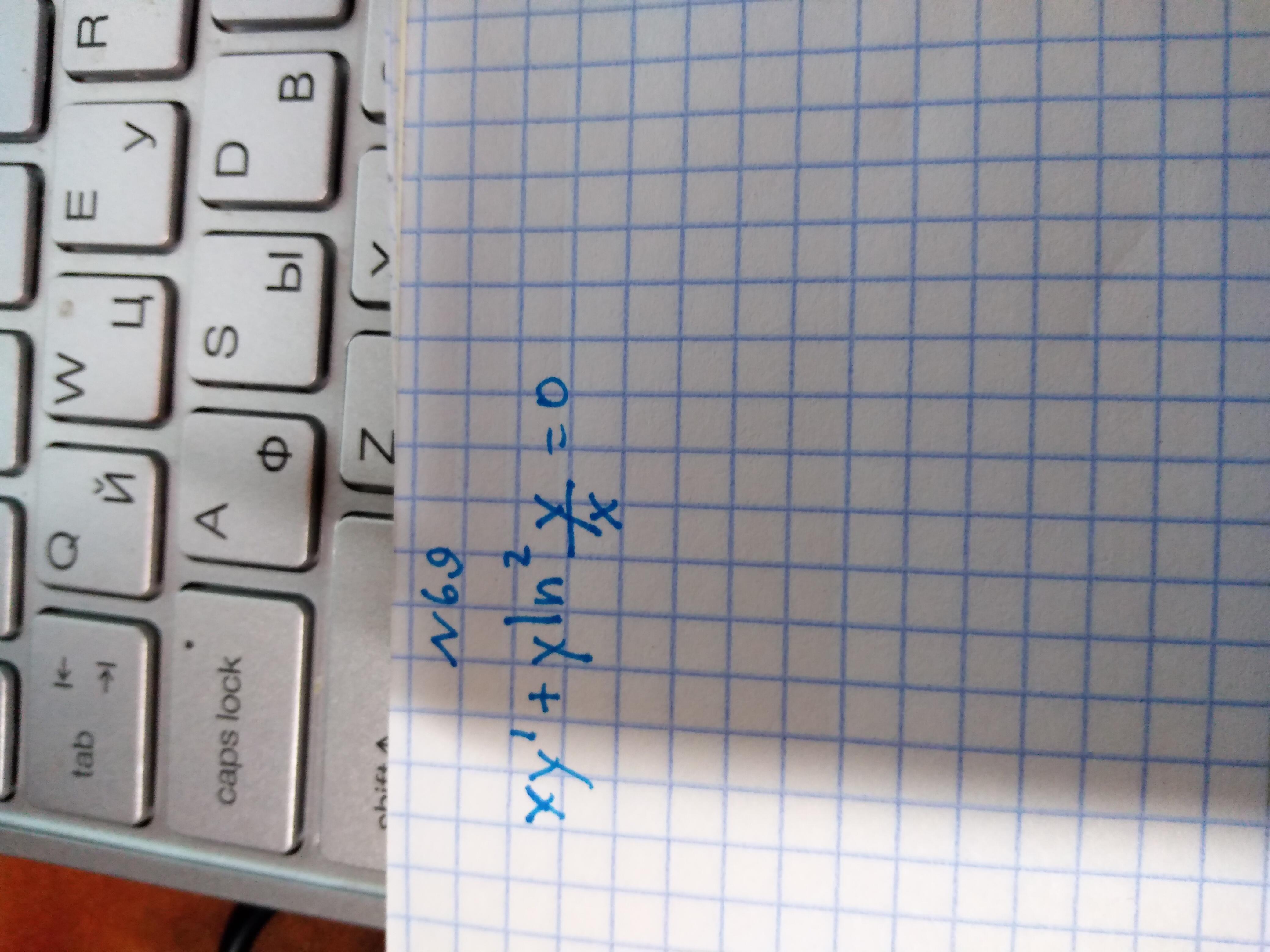
Ответы
Автор ответа:
0
Ответ:
разделим на х:
это однородное ДУ
Замена:
общее решение
Похожие вопросы
Предмет: Русский язык,
автор: svetaglushckov
Предмет: Математика,
автор: Аноним
Предмет: География,
автор: софа31
Предмет: Алгебра,
автор: нескажу2005
Предмет: Математика,
автор: MALIFISENTA000