Предмет: Алгебра,
автор: lyubomirsky
Решите систему уравнения
Приложения:
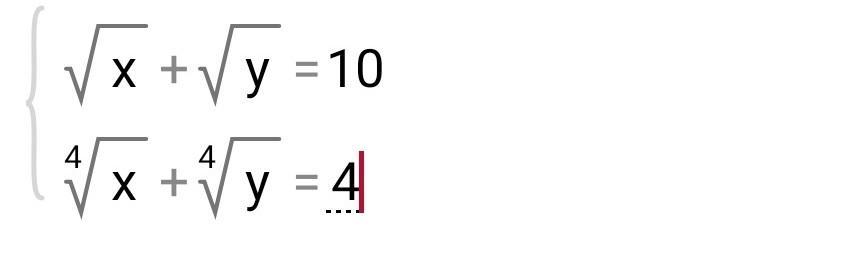
Ответы
Автор ответа:
1
Объяснение:
Пусть ⁴√x=t ⁴√y=v. ⇒
Ответ: (1;81), (81;1).
lyubomirsky:
Спасибо)
Удачи.
Похожие вопросы
Предмет: История,
автор: dashatitova00
Предмет: Математика,
автор: kavprok
Предмет: Геометрия,
автор: tanyatanyaaaaaa1
Предмет: Литература,
автор: feg430
Предмет: Биология,
автор: Геог2мафия