Предмет: Математика,
автор: annatulay007
Обчислити площу фігури, обмеженої графіком функції
y = 1 - x⁴ та віссю Оx.
будь ласка, напишіть пояснення до розв'язку)
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
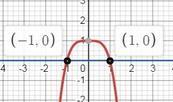
строим графики функций и определяем фигуру, пределы интегрирования
по графику находим все нужные значения для формулы площади
у нас: x изменяется от -1 до 1 ⇒ x₁ = -1; х₂ = 1
за у₁ принимают функцию, лежащую на графике "выше" другой
у нас: у₁ = 1-х⁴ ; у₂ = 0 (ось ОХ задается функцией у = 0)
вот и всё. теперь считаем площадь
Приложения:
Похожие вопросы