Question

Розв’язати нерівність:

1) x
^2+3x–4 < 0;

2) x^
2 + x + 1 >0.
​

Answer 1

Ответ:

1) x∈(-4;1)

2) x∈(-∞;+∞)

Объяснение:

1) x^2 + 3x - 4 < 0

приравниваем к 0

x^2 + 3x - 4 = 0

по т. Виета

x1 + x2 = -3   x1 = -4

x1 * x2 = -4 → x2 = 1

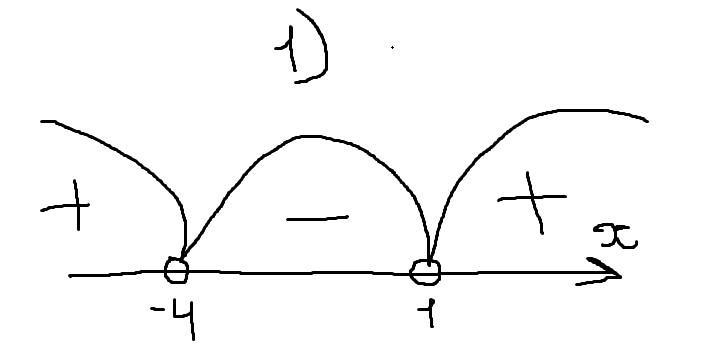
Теперь рисуем прямую x,выделяем на ней выколотые точки 1 и -4 (картинку прикрепил)

Нам нужно,чтобы значения выражения было отрицательным.

И получаем

x∈(-4;1)

=========================================

2) x^2 + x + 1 > 0

здесь получится так,что какое бы мы число не взяли - неравенство будет верным.

Поэтому x∈(-∞;+∞)

=========================================