Предмет: Математика,
автор: DeadNorth
Помогите пожалуйста, нужно найти производную
Приложения:
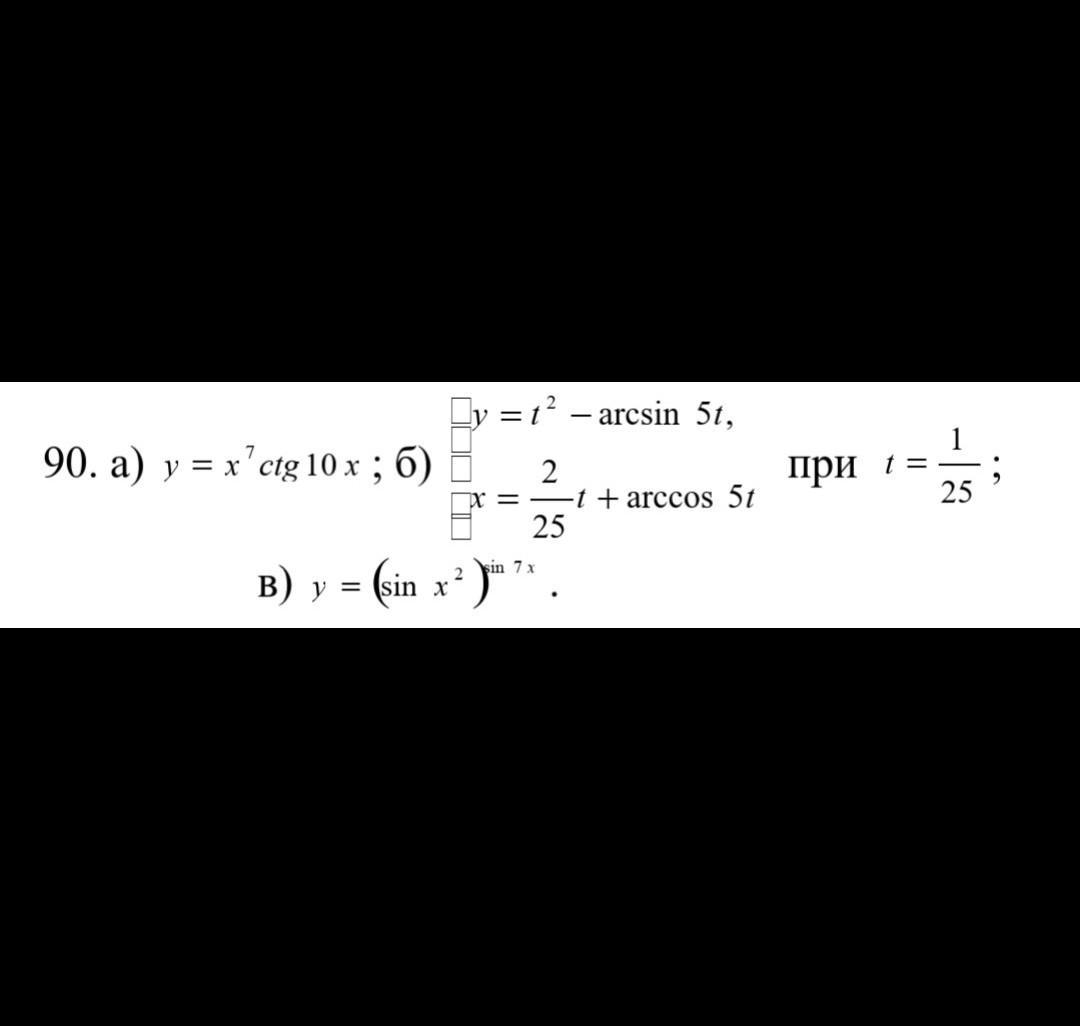
Ответы
Автор ответа:
1
Ответ:
а)
б)
при t = 1/25
в)
формула:
Похожие вопросы
Предмет: Алгебра,
автор: Кержакова14
Предмет: Русский язык,
автор: sandra02ru
Предмет: Русский язык,
автор: Аолаоушслао
Предмет: Алгебра,
автор: wicenatos
Предмет: Литература,
автор: pugolovkina16