Предмет: Математика,
автор: mishadr2
СРОЧНО!!! Помогите найти общее решение Дифференциального уравнения
Приложения:
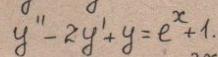
Ответы
Автор ответа:
0
Ответ:
1) Решаем ОЛДУ:
замена:
2) Подбираем у с неопределенными коэффициентами:
умножаем на х^2, так как в общем решении ОЛДУ два слагаемых с е^х.
Подставляем в НЛДУ:
Отсюда:
A = 1
2B = 1 ; B = 1/2
Получаем:
общее решение:
Похожие вопросы
Предмет: Русский язык,
автор: мир20
Предмет: Математика,
автор: kf2005
Предмет: Алгебра,
автор: deadend08
Предмет: Математика,
автор: kazjavo4ka08p2aqj7