Предмет: Математика,
автор: skillzevils
Помогите пожалуйста решить =(
Приложения:
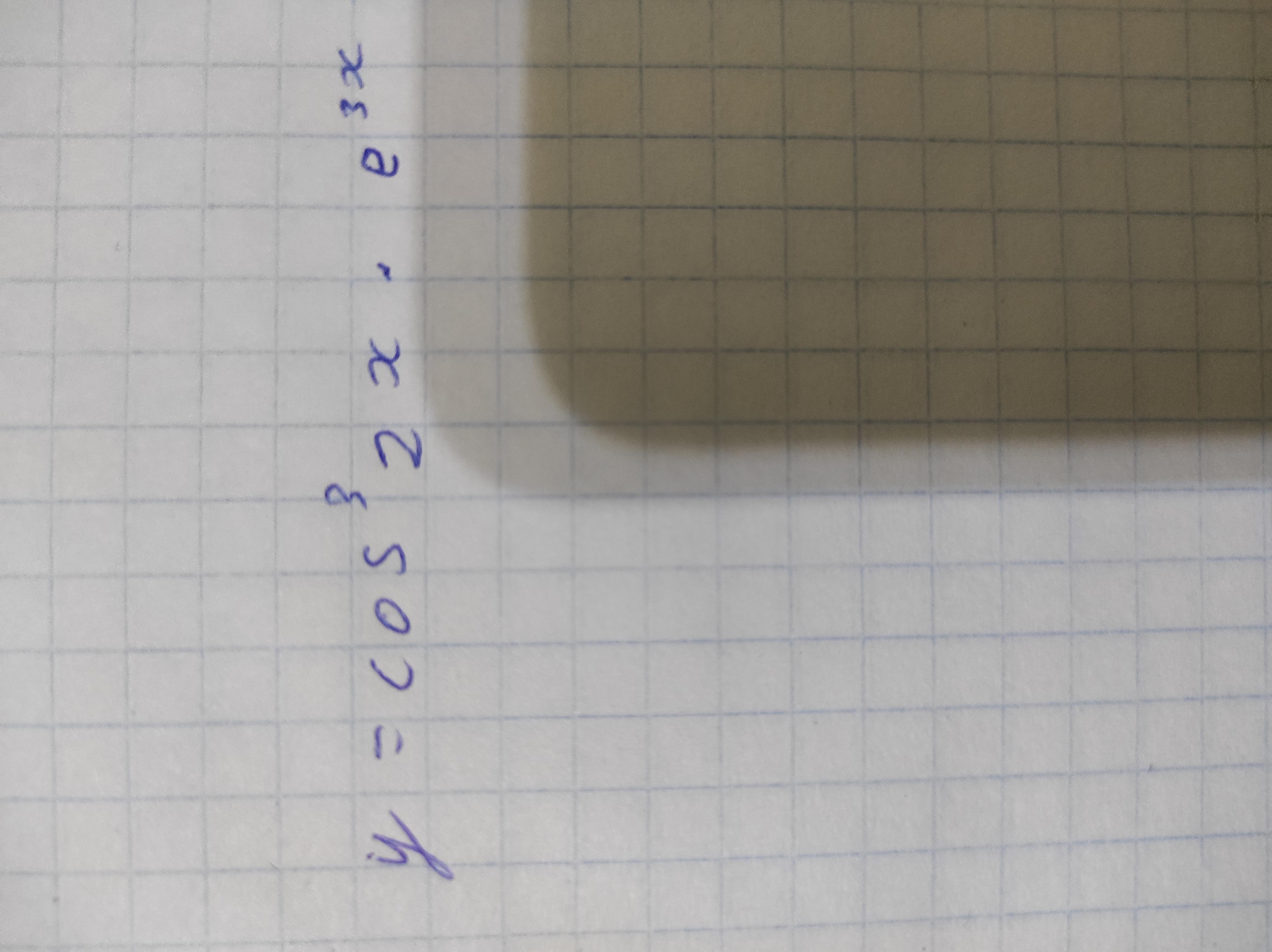
Miroslava227:
что нужно сделать?
Расписать чему равен y'
Ответы
Автор ответа:
1
Ответ:
Автор ответа:
1
Ответ:
Пошаговое объяснение:
прервём запись
и вернёмся обратно к производной
Огромное спасибо за пошаговое объяснение
Похожие вопросы
Предмет: Химия,
автор: космэля
Предмет: Геометрия,
автор: AnnaGumenyk
Предмет: Русский язык,
автор: amina210300
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: 1234567891253