Предмет: Математика,
автор: golovanwo
Найти производные данных функций.
Приложения:
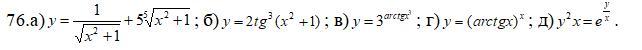
Ответы
Автор ответа:
0
Ответ:
а)
б)
в)
г)
д)
Похожие вопросы
Предмет: Математика,
автор: cebanova04
Предмет: География,
автор: valeriatopal20
Предмет: Математика,
автор: densen1221
Предмет: Математика,
автор: dima4343
Предмет: Математика,
автор: Саня2034