Question

Найдите фокальные радиусы эллипса симметричного относительно осей координат, проходящего через точку M(-4; Корень из 21), фокусы которого находятся на оси Ox, эксцентриситет равен 3/4. В ответе укажите сумму длин фокальных радиусов.

Answer 1

Эксцентриситет е равен: е = с/а  или с= еа.

Свойство эллипса: а² + b² = c².

Заменим  c² = е²а² и подставим: а² + b² = е²а².

Преобразуем: а²(1 - е²) = b²,

или  b² = а²(1 - е²) = а²(1 - (3/4)²) = а²(1 - (9/16)).

Используем уравнение эллипса (x²/a²) + (y²/b²) = 1 и координаты точки

М (-4; √21).

((-4)²/a²) +((√21)²/а²(1 - (9/16))) = 1.

Отсюда получаем 7а² = 7*16 + 21*16 = 16*28, сократим: а² = 64, а = 8.

b² = 64*(1 - (9/16)) = 28.

c = √(a² - b²) = √(64 - 28) = √36 = 6.

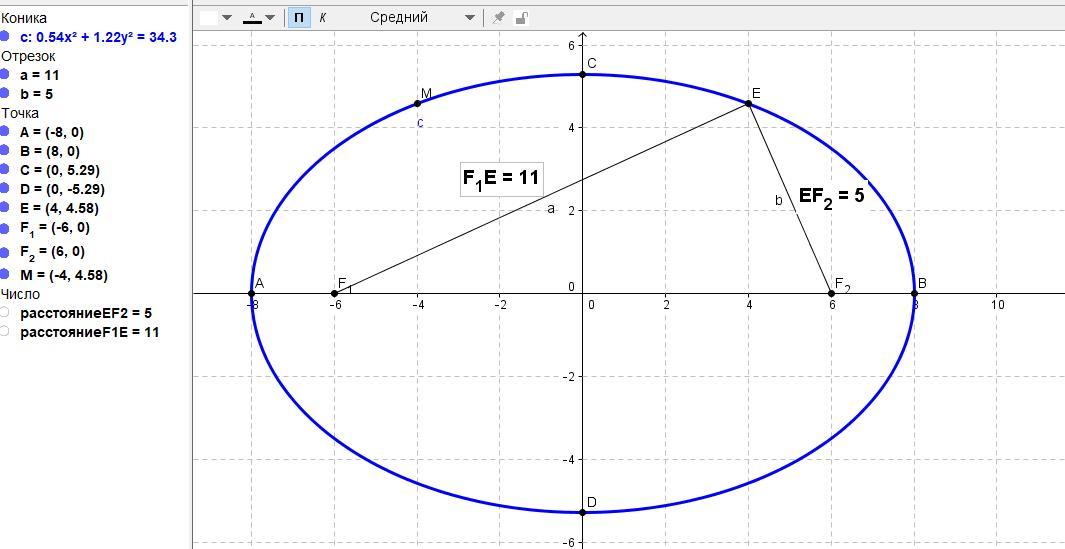
Фокальные радиусы - это отрезки, соединяющие любую точку эллипса с его фокусами.

$r_1,_2=a+-ex.$

Сумма их величина постоянная и равна 2а.