Предмет: Геометрия,
автор: f1ngo
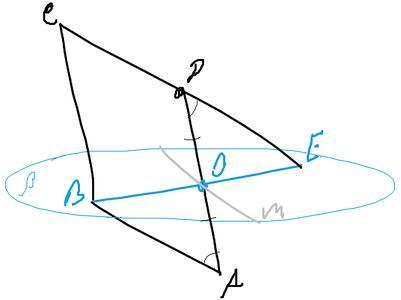
Дан параллелограмм АВСD в котором прямая АD лежит в плоскости α. А прямая ВС не лежит в плоскости α. Точка О середина АD. Прямая m проходит через точку О и перпендикулярна АD, а так же лежит в плоскости α. Докажите, что прямая m и точка В могут лежать в одной плоскости β. Докажите, что прямая СD пересекает плоскость β в некоторой точке Е. Найдите СЕ если АВ = а, АД = b
Ответы
Автор ответа:
0
Через две параллельные проходит плоскость, параллелограмм лежит в плоскости.
Прямые BO и CD пересекаются в плоскости параллелограмма в точке E.
Треугольники AOB и DOE равны по стороне и прилежащим углам.
AB=DE=CD =a => CE=2a
Прямая (m) и точка (B) всегда лежат в одной плоскости (по аксиоме).
Плоскость параллелограмма и плоскость b пересекаются по прямой BE (т.е. не имеют других общих точек).
Точка С не лежит на прямой BE, следовательно не лежит в плоскости b.
Прямая CE не лежит в плоскости b, но пересекает ее в точке E.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: marena98
Предмет: Русский язык,
автор: aprasovskayaanya896
Предмет: Биология,
автор: lerochka32
Предмет: Литература,
автор: fariza05555
Предмет: Математика,
автор: арина5510