Предмет: Математика,
автор: bycarovarsenij
решите системное уравнение (ответ (1;81); (81;1)
Приложения:
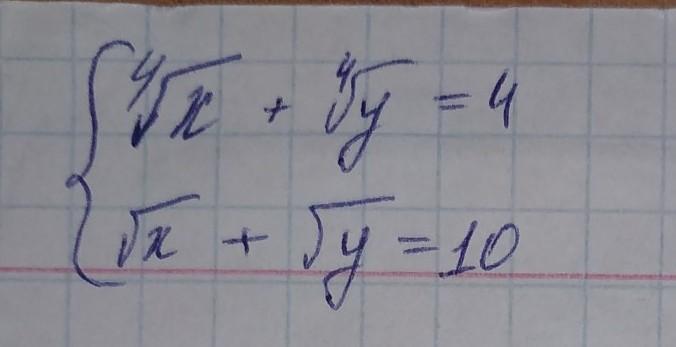
Ответы
Автор ответа:
2
Для удобства введём две замены: и
.
Решим верхнее уравнение системы отдельно.
Подкоренное выражение всегда неотрицательно.
Продолжаем решение уравнения.
Возведём обе части уравнения в квадрат.
Снова возведём обе части в квадрат.
По теореме Виета:
Подставляем каждое значение и находим
:
Обратная замена:
Данная система имеет две пары решений.
Ответ: .
Veronika724:
Так можно решить и через корни четвертой степени, но лично мне неудобно с ними таскаться.
спасибо
Похожие вопросы
Предмет: Українська мова,
автор: katiyv19
Предмет: Алгебра,
автор: Мэлани01
Предмет: Математика,
автор: sashagrey98
Предмет: Математика,
автор: вася800