Предмет: Математика,
автор: evgenij55555
Приведите уравнение кривой второго порядка к каноническому виду и постройте ее.
Укажите координаты вершин и фокусов. Напишите уравнение директрисы и асимптот,
если они есть. Вычислите эксцентриситет кривой.
Приложения:
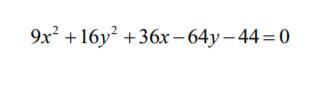
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
9x²+16y²+36x-64y-44=0⇒9(x²+4x)+16(y²-4y)-44=0⇒9(x²+4x+4-4)+16(y²-4y+4-4)-44=0⇒9(x²2+4x+4)-36+16(y²-4y+4)-64-44=0⇒9(x+2)²+16(y-2)²=144⇒9(x+2)²/144+16(y-2)²/144=144/144⇒(x+2)²/16+(y-2)²=1⇒
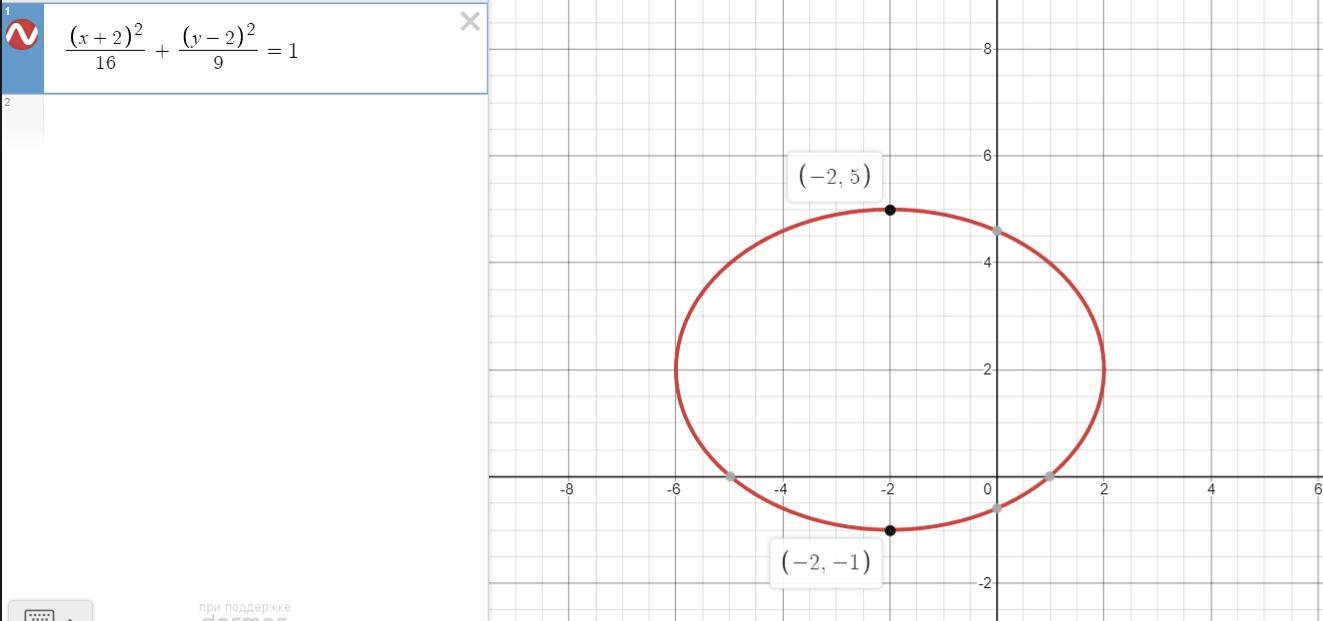
(x+2)²/4²+(y-2)²/3²=1
это каноническое уравнение эллипса с центром в точке О(-2;2)
координаты вершин А₁(-4-2;0+2)=(-6;2), А₂(4-2;0+2)=(2;2), В₁(0-2;-3+2)=(-2;-1), В₂(0-2;3+2)=(-2;5)
координаты фокусов F₁=(-√(16-9)-2;0+2)=(-√5-2;2), F₂(√5-2;2)
ексцентриситет ε=√5/4
уравнения директрис х+2=-4/(√5/4)=-16/√5⇒х=-16/√5-2 и х=16/√5-2
Приложения:
Похожие вопросы
Предмет: Математика,
автор: semsasha888
Предмет: Алгебра,
автор: Аноним
Предмет: Физика,
автор: elitamikuckaja
Предмет: Математика,
автор: про805