Предмет: Алгебра,
автор: ilyyyyy54
ПОМОГИТЕ С ПРОИЗВОДНЫМИ,НЕ ПОНИМАЮ НИЧЕРТА
СРОЧНО НАДО!!!!
Приложения:
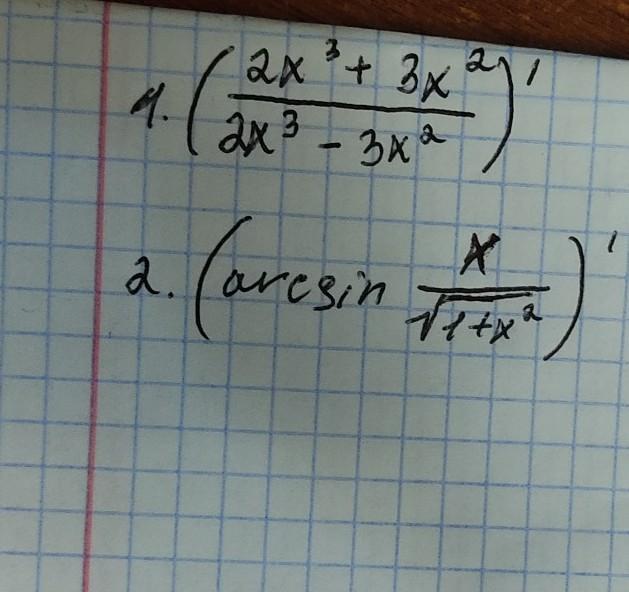
Ответы
Автор ответа:
0
Объяснение:
1)
Ответ: .
2)
Надо воспользоваться формулой:
Ответ: .
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: nastyanikitina19
Предмет: Химия,
автор: dmb20092
Предмет: История,
автор: катя5612
Предмет: Алгебра,
автор: PeryaZ