Предмет: Математика,
автор: dimans51
Дифференциальные уравнения
Приложения:
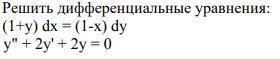
Ответы
Автор ответа:
1
Ответ:
1)
общее решение
2)
замена:
общее решение
Похожие вопросы
Предмет: Русский язык,
автор: mtitova1983
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: kuzmitania2011
Предмет: Физика,
автор: Aderevnina24