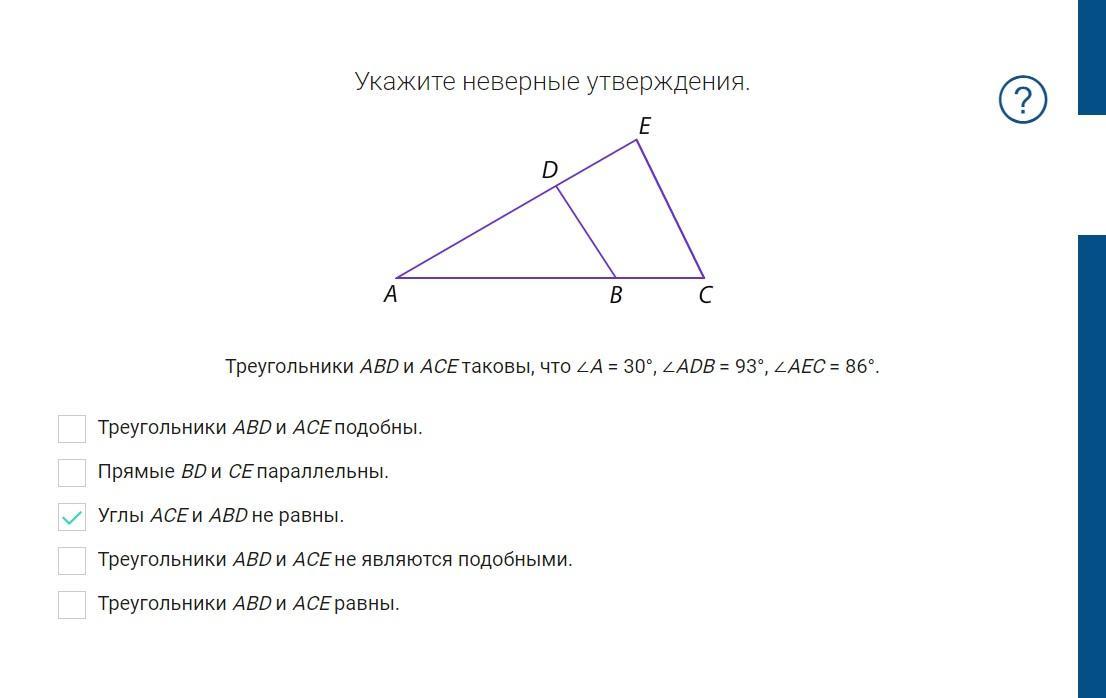
Укажите неверные утверждения.
Треугольники AВD и АСЕ таковы, что ∠А = 30°, ∠АDВ = 93°, ∠АЕС = 86°.
Треугольники AВD и АСЕ подобны.
Прямые ВD и СЕ параллельны.
Углы ACE и ABD не равны.
Треугольники AВD и АСЕ не являются подобными.
Треугольники AВD и АСЕ равны.
Ответы
Дано: ΔABD; ΔACE;
∠A = 30°; ∠ADB = 93°; ∠AEC = 86°
Решение:
Сумма углов треугольника равна 180°.
ΔABD: ∠A + ∠ADB + ∠ABD = 180°
∠ABD = 180° - ∠A - ∠ADB = 180° - 30° - 93° = 57°
ΔAEC: ∠A + ∠AEC + ∠ACE = 180°
∠ACE = 180° - ∠A - ∠AEC = 180° - 30° - 86° = 64°
Проверим признак подобия треугольников: если два угла одного треугольника равны двум углам второго треугольника, то такие треугольники подобны.
ΔACE: ∠A = 30°; ∠AEC = 86°; ∠ACE = 64°
ΔABD: ∠A = 30°; ∠ADB = 93°; ∠ABD = 57°
В треугольниках нет двух равных углов, то есть треугольники не подобны.
Треугольники ABD и ACE подобны: НЕВЕРНО.
Признак параллельности прямых: если при пересечении двух прямых секущей соответственные углы равны, то такие прямые параллельны.
Две прямые BD и CE, секущая AE, соответственные углы:
∠ADB = 93°; ∠AEC = 86° ≠ 93°.
Соответственные углы не равны, значит, прямые BD и CE не параллельны.
Прямые BD и CE параллельны: НЕВЕРНО.
Углы ACE и ABD не равны: ВЕРНО.
Треугольники ABD и ACE не являются подобными: ВЕРНО.
Равные треугольники при наложении совпадают. Треугольник AEC при наложении больше треугольника ADB.
Треугольники ABD и ACE равны: НЕВЕРНО.