Предмет: Математика,
автор: gtv79875
найдите область определения функции 
найдите область определения функции 
gtv79875:
это 2 разных функции
Ответы
Автор ответа:
1
Ответ:
========================================
Пошаговое объяснение:
Приложения:
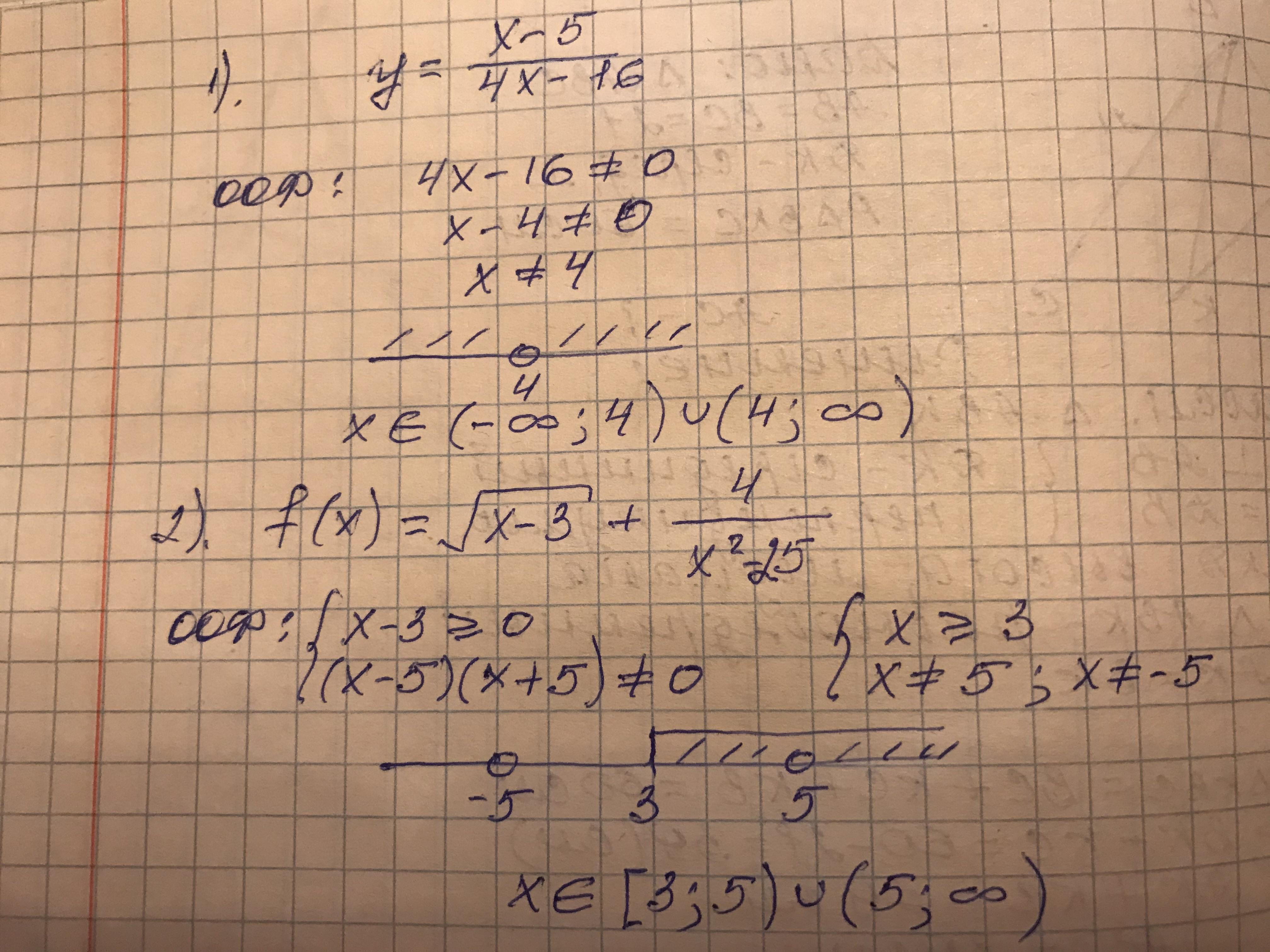
Автор ответа:
1
Ответ:
Пошаговое объяснение:
1) у= х-5/ 4х-16
D(y): 4х-16≠0 ⇒4х≠16 ⇒ х≠16:4 ⇒х≠4, значит D(y)=(-∞;4)∪(4;+∞)
2) f(x)= √(x-3) + 4/(x²-25)
D(f): 1) x-3≥0 и 2)х²-25≠0 (можно объединить эти 2 условия в систему неравенств)
1) x-3≥0 и 2)х²-25≠0
х≥3 х²≠25
х≠±5
Значит D(y)=[3;5)∪(5;+∞)
Похожие вопросы
Предмет: Литература,
автор: tanchik2121985
Предмет: Математика,
автор: anna180602
Предмет: Другие предметы,
автор: edaru
Предмет: Физика,
автор: demmarik
Предмет: Алгебра,
автор: kellyone1