Предмет: Математика,
автор: anton2004323
Помогите пожалуйста с математикой. хелп ми)
Приложения:

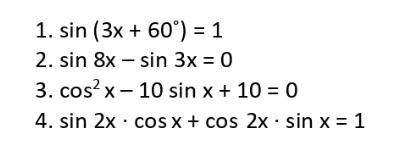
minaraalieva2008:
хз
Ответы
Автор ответа:
0
Ответ:
1.
n принадлежит Z.
2.
замена:
n принадлежит Z.
3.
n принадлежит Z .
4.
n принадлежит Z.
____________
1.
n принадлежит Z.
2.
n принадлежит Z.
3.
замена:
нет корней
4.
это формула суммы углов синуса.
n принадлежит Z.
Автор ответа:
0
Ответ:n принадлежит Z.
Пошаговое объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: Юляша321
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: mehkrinisa
Предмет: Математика,
автор: ayedilova
Предмет: Математика,
автор: toxxxa333