Предмет: Математика,
автор: kabylbekov2424
исследовать сходимость ряда с помощью признака Даламбера
помогите решить пожалуйста
Приложения:
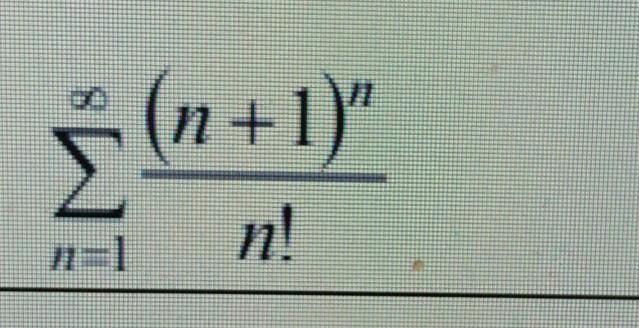
Ответы
Автор ответа:
1
Ответ:
kabylbekov2424:
спасибо
там ещё внизу один вопрос есть помогите решить пожалуйста
пожалуйста
ещё один вопрос есть
помогите решить срочно пожалуйста
Похожие вопросы
Предмет: Химия,
автор: Ruslan1712
Предмет: Математика,
автор: kristinagerasi1
Предмет: Алгебра,
автор: komarovskayiri
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: ьчьалига4