Предмет: Математика,
автор: vk131672
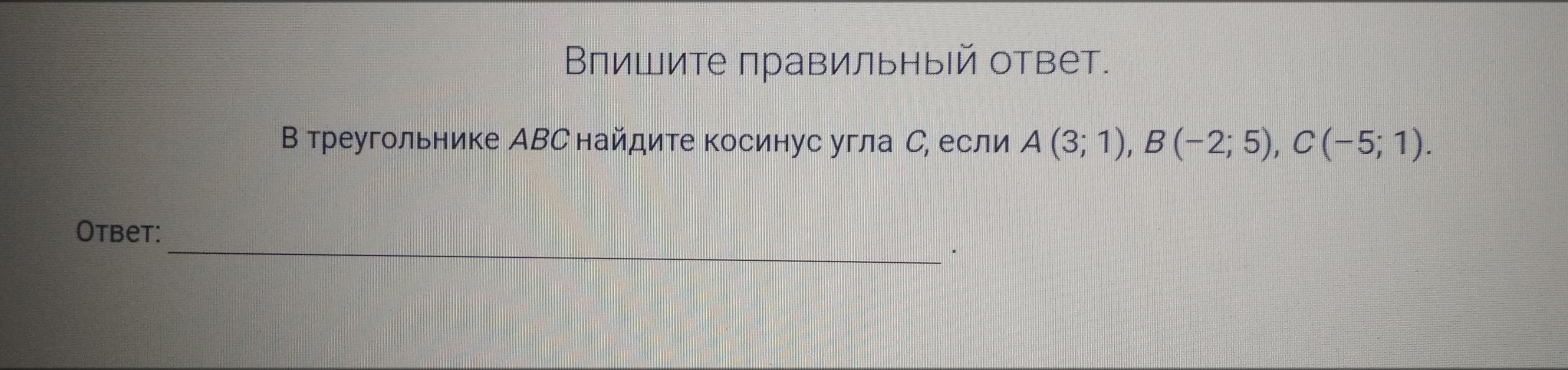
Помогите пожалуйста.
Приложения:
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Расстояние между двумя точками (длина отрезка):
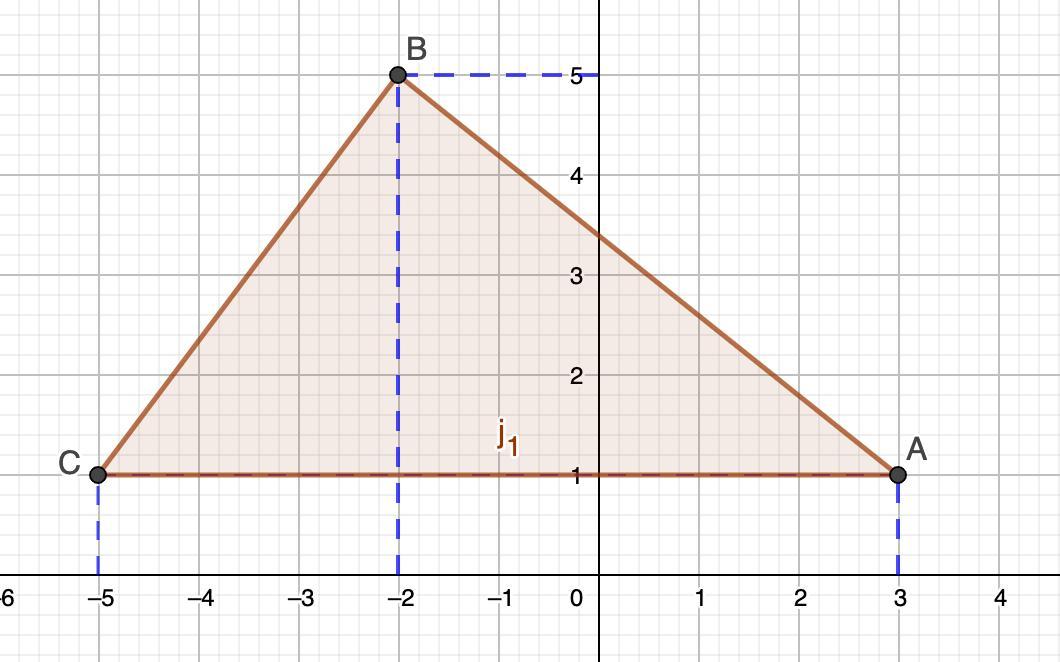
Построим треугольник и найдем длины его сторон:
Найдем cos∠C, используя теорему косинусов:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Vilka435623
Предмет: Русский язык,
автор: strizka
Предмет: Геометрия,
автор: k4karina
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: ddxxrdsxxч